Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=góc BAD=90 độ
b; AH vuông góc BC
DE vuông góc BC
=>AH//DE
a: Xét ΔBAM và ΔBDM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó; ΔBAM=ΔBDM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó; ΔBAD=ΔBED
=>DA=DE và góc BED=90 độ
=>DE vuông góc với BC
b: AH vuông góc với BC
DE vuông góc với BC
Do đó: AH//DE
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC
a: Xét ΔBAD vàΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=90 độ
=>DE vuông góc BC
b: BA=BE
DA=DE
=>BD là trung trực của AE
=>BD vuông góc AE
c: AM//DE
DE vuông góc BC
=>AM vuông góc BC
AM//DE
=>góc MAE=góc AED
=>góc MAE=góc DAE
=>AE là phân giác của góc MAD
\(B=\frac{1}{4}\left(a^2b^2\right)2ab\) tại a = 1, b = |2|
\(B=\frac{1}{4}\left(1^2.2^2\right)2.1.2\)
\(B=\frac{1}{4}.4.2.1.2\)
\(B=4\)
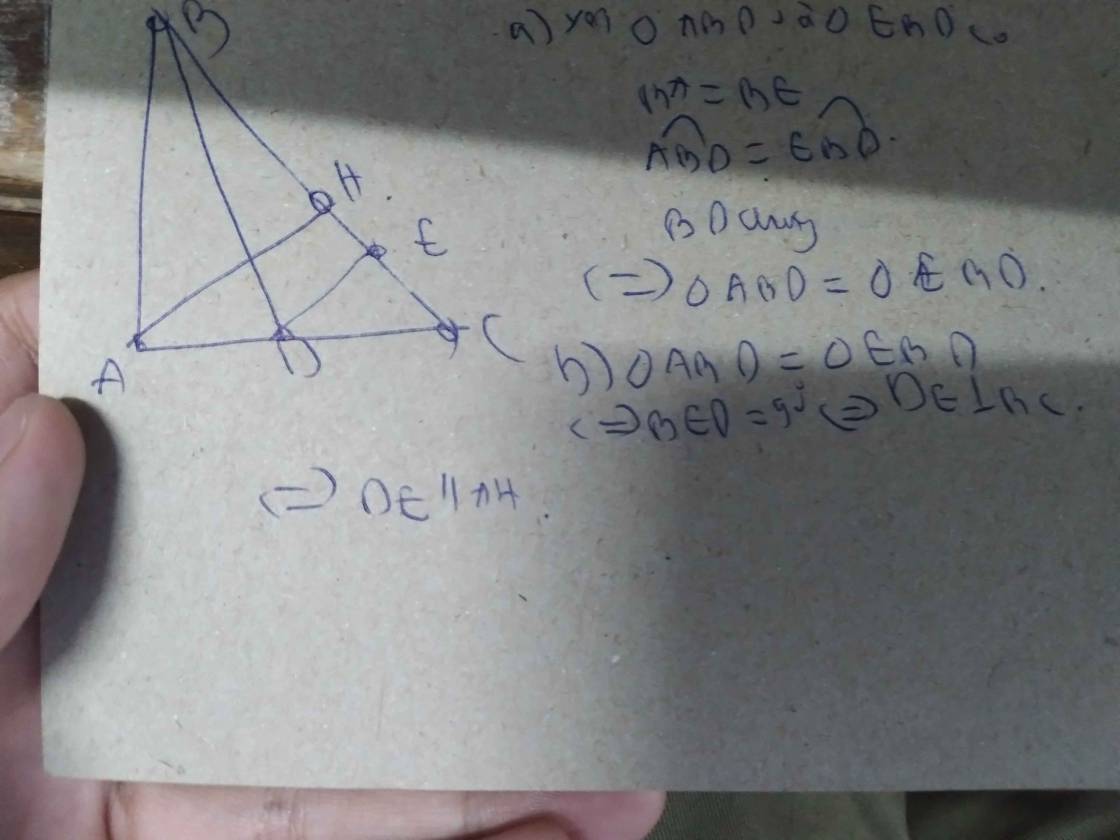
mn ơi giup mik vs
gấp lắm r mn ơii