Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=góc BAD=90 độ
b; AH vuông góc BC
DE vuông góc BC
=>AH//DE

a: Xét ΔBAM và ΔBDM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó; ΔBAM=ΔBDM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó; ΔBAD=ΔBED
=>DA=DE và góc BED=90 độ
=>DE vuông góc với BC
b: AH vuông góc với BC
DE vuông góc với BC
Do đó: AH//DE

mik làm lại cho nó lq được ko?
a) ta xét t/gABM và t/gDBM ta có:
AB=DB (gt)
=>^ABM=^DBM
BM chung
=>t/gABM=t/gDBM (c.g.c)
b)Vì t/gABM=t/gDEM
=>AM=DM ( 2 cạnh tương ứng)
=>^MAD=^AMD=90o
=>MD_|_BC
c)Vì t/gABM=t/gDEM (đối đỉnh)
=>t/gAME=t/gDMC(cgv-gn)
=>ME=MC
=>t/gMEC cân tại M
=>^MEC=^MCE
Mà trong t/gMEC ta thấy:
^MEC+^MDA+^DAM=^MEC+^CEM+EMC
mà ^EMC=^AMD ( 2 góc đối đỉnh)
=>^MAD+^MDA=^MEC+^EMC
=>^MAD=^MCE ( so le)
=>AD//CE
=>đpcm.
a) tam giác ABM=tam giác DBM (c.g.c) (1) suy ra AM=MD
b) Từ (1) suy ra góc BAM = góc BDM
mà góc BAM = 900
suy ra góc BDM = 900
suy ra MD vuông góc với BC tại D
c) Vì AB=BD suy ra tam giác ABD cân tại B
mà BM là phân giác của góc ABD
suy ra BM là phân giác đồng thời là đường cao của tam giác ABD
suy ra BM vuông góc với AD (3)
Xét tam giác AME và tam giác DMC
có góc MAE=góc MDC=900
AM=MD ( CMT)
góc AME=góc DMC ( đối đỉnh)
suy ra tam giác AME = tam giác DMC (g.c.g)
suy ra AE=DC
mà AB+AE=BE, BD+DC=BC lại có AB=BD
suy ra BC = BE suy ra tam giác EBC cân tại B
mà BM là phân giác của góc EBC
suy ra BM là phân giác đồng thời là đường cao của tam giác EBC
suy ra BM vuông góc với CE tại M (4)
Từ (3) và (4) suy ra AD//CE

a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC

a: Xét ΔBAD vàΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=90 độ
=>DE vuông góc BC
b: BA=BE
DA=DE
=>BD là trung trực của AE
=>BD vuông góc AE
c: AM//DE
DE vuông góc BC
=>AM vuông góc BC
AM//DE
=>góc MAE=góc AED
=>góc MAE=góc DAE
=>AE là phân giác của góc MAD

\(B=\frac{1}{4}\left(a^2b^2\right)2ab\) tại a = 1, b = |2|
\(B=\frac{1}{4}\left(1^2.2^2\right)2.1.2\)
\(B=\frac{1}{4}.4.2.1.2\)
\(B=4\)
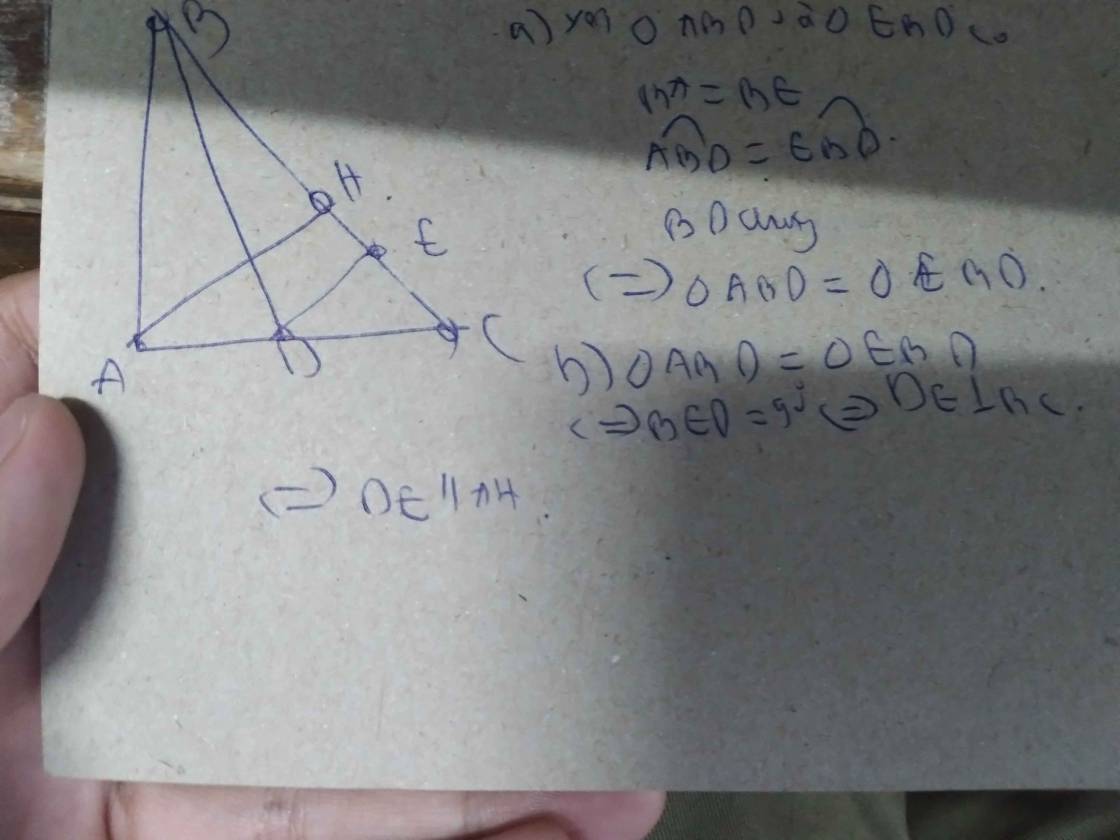
mn ơi giup mik vs
gấp lắm r mn ơii