Cho hình thang ABCD ( AD song song BC ).Gọi AC là tia phân giác của góc A. CM : AB = BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 8 2022
Bài 2:
Gọi AI là phân giác của góc BAD
Xét ΔDAI có góc DAI=góc DIA
nên ΔDIA cân tại D
=>DA=DI
=>CB=CI
=>ΔCBI cân tại C
=>góc CBI=góc CIB
=>góc CBI=góc ABI
=>BI là phân giác của góc ABC(ĐPCM)
UN
1
26 tháng 7 2015
Vì AD//BC
=> góc DAC = góc BCA. ( so le trong)
Mà góc DAC = góc BAC ( AC là p/giác góc A)
=>góc BAC= goc BCA
=> tam giác BAC cân tại B
=>AB=BC
Vậy _____________
6 tháng 8 2022
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
3 tháng 7 2023
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
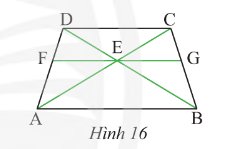
Vì \(EG\) // \(AB\) (gt)
suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)
Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:
\(AC = BD\) (tính chất hình thang cân)
\(BC = AD\) (tính chất hình thang cân)
\(AB\) chung
Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)
Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)
Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)
có sai đề ko ????
hình như có sai đề ko thì phải bn