Câu 1. Cho 11 g hỗn hợp Al, Fe phản ứng hoàn toàn với lượng dư dung dịch H,SO4 đặc nóng thu được 11,1555 L SO2 (sản phẩm khử duy nhất, ở đkc ) và dung dịch A. Tính % theo khối lượng của mỗi kim loại trong hỗn hợp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
28 tháng 8 2021
a)
nSO2=\(\dfrac{10,08}{22,4}\)= 0,45(mol)
2Al + 6H2SO4 --> Al2(SO4)3 + 6H2O +3SO2
x ---------------------------------------------> 3/2x
2Fe + 6H2SO4 --> Fe2(SO4)3 + 6H2O + 3SO2
y --------------------------------------------------> 3/2y
b) ta có hệ pt sau
\(\left\{{}\begin{matrix}27x+56y=11\\\dfrac{3}{2}x+\dfrac{3}{2}y=0,45\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x=0,2\\y=0,1\end{matrix}\right.\)
%mAl = \(\dfrac{0,2.27}{11}.100\)= 49%
%mFe=\(49-100\) =51%
c) m Al2(SO4)3= 0,1.342=34,2 g
mFe2(SO4)3=0,05.400=20 g
9 tháng 5 2021
- Gọi số mol Al và Fe trong hốn hợp lần lượt là a, b mol
PTKL : 27a + 56b = 22
BTe : 3a + 3b = 1,8
=> a = 0,4 và b = 0,2 .
=> mAl = 10,8g và mFe = 11,2 g
b, Sau phản ứng thu được muối Al2(SO4)3 và Fe2(SO4)3 .
=> mM = 108,4g
MN
9 tháng 5 2021
\(n_{Al}=a\left(mol\right),n_{Fe}=b\left(mol\right)\)
\(\Rightarrow27a+56b=22\left(1\right)\)
\(n_{SO_2}=\dfrac{20.16}{22.4}=0.9\left(mol\right)\)
\(2Fe+6H_2SO_{4\left(đ\right)}\rightarrow Fe_2\left(SO_4\right)_3+3SO_2+6H_2O\)
\(2Al+6H_2SO_{4\left(đ\right)}\rightarrow Al_2\left(SO_4\right)_3+3SO_2+6H_2O\)
\(n_{SO_2}=1.5a+1.5b=0.9\left(mol\right)\left(2\right)\)
\(\left(1\right),\left(2\right):a=0.4,b=0.2\)
\(m_{Al}=0.4\cdot27=10.8\left(g\right)\)
\(m_{Fe}=11.2\left(g\right)\)
\(m_{Muối}=0.2\cdot342+0.1\cdot400=108.4\left(g\right)\)
MN
1 tháng 8 2021
\(n_{Cu}=a\left(mol\right),n_{Fe}=b\left(mol\right)\)
\(m_X=64a+56b=16.2\left(g\right)\left(1\right)\)
\(n_{SO_2}=\dfrac{8.96}{22.4}=0.4\left(mol\right)\)
Bảo toàn e :
\(2a+3b=0.4\cdot2=0.8\left(2\right)\)
\(\left(1\right),\left(2\right):a=0.0475,b=0.235\)
\(\%Cu=\dfrac{0.0475\cdot64}{16.2}\cdot100\%=18.76\%\)
\(\%Fe=81.24\%\)
\(b.\)
\(\dfrac{a}{b}=\dfrac{0.0475}{0.235}=\dfrac{19}{94}\)
\(\Rightarrow n_{Cu}=19x\left(mol\right),n_{Fe}=94x\left(mol\right)\)
\(m_X=19x\cdot64+94x\cdot56=22\left(g\right)\)
\(\Rightarrow x=\dfrac{11}{3240}\)
\(n_{H_2}=n_{Fe}=\dfrac{11}{3240}\cdot94=\dfrac{517}{1620}\left(mol\right)\)
\(V_{H_2}=7.15\left(l\right)\)
TP
20 tháng 8 2021
\(n_{SO_2}=\dfrac{13,644}{22,4}=0,61\left(mol\right)\)
Đặt n Fe = x (mol) =>\(m_{Fe}=56x\)
Vì m Fe = mMg => \(n_{Mg}=\dfrac{56x}{24}=\dfrac{7}{3}x\)
nAl = y(mol)
=> 56x + 56x + 27y = 16,14 (1)
\(Fe\rightarrow Fe^{3+}+3e\) \(S^{+6}+2e\rightarrow S^{+4}\)
\(Mg\rightarrow Mg^{2+}+2e\)
\(Al\rightarrow Al^{3+}+3e\)
Bảo toàn e : 3x + \(\dfrac{7}{3}.2x\) + 3y = 0,61.2 (2)
Từ (1), (2) => x=0,12 ; y=0,1
=> mFe =mMg=0,12.56 = 6,72(g)
m Al = 0,1.27=2,7(g)
H
16 tháng 8 2021
Gọi $n_{Fe} = a ; n_{Mg} = b; n_{Al} = c$
Ta có :
$24b = 56a(1)$
$56a + 24b + 27c = 16,14(2)$
$n_{SO_2} = 0,61(mol)$
Bảo toàn electron : $3n_{Fe} + 2n_{Mg} + 3n_{Al} = 2n_{SO_2}$
$\Rightarrow 3a + 2b + 3c = 0,61.2(3)$
Từ (1)(2)(3) suy ra a = 0,12 ; b = 0,28 ; c = 0,1
$m_{Fe} = m_{Mg} = 0,12.56 = 6,72(gam)$
$m_{Al} = 0,1.27 = 2,7(gam)$
25 tháng 11 2017
Chọn A
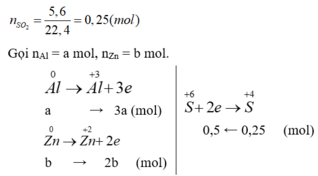
Ta có: m h h = 9 , 2 g → 27a + 65b = 9,2 (*)
Bảo toàn số mol electron có: 3a + 2b = 0,5 (**)
Giải (*), (**): a = b = 0,1 mol.
m A l = 0 , 1 . 27 = 2 , 7 g a m
30 tháng 1 2017
Đáp án A.
Gọi nAl = a mol, nZn = b mol.
Ta có: 27a + 65b = 9,2 (*)
3a + 2b = 0,5 (**)
Giải (*), (**): a = b = 0,1 mol.
mAl = 0,1.27 = 2,7 gam
Ta có: 27nAl + 56nFe = 11 (1)
\(n_{SO_2}=0,45\left(mol\right)\)
BT e, có: \(3n_{Al}+3n_{Fe}=2n_{SO_2}=0,9\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,2\left(mol\right)\\n_{Fe}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,2.27}{11}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)