Mọi người giúp mình bài 6 với ( câu a,b,c) :<
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)


Bài 2:
a)|x| < 3
x\(\in\){-2;-1;0;1;2}
b)|x - 4 | < 3
x\(\in\){ 6 ; 5 ; 4 ; 3 ; 2 }
c) | x + 10 | < 2
x\(\in\){ -2 ; -10 }
Bài 1:
A = 1 + 2 - 3 + 4 + 5 - 6 +...+98 - 99
A = (1 + 4 + 7 +...+97) + [(2-3)+(5-6)+...+(98-99)]
A = 1617 + [(-1)+(-1)+...+(-1)]
A = 1617 + (-49)
A = +(1617-49) = A = 1568
B = - 2 - 4 + 6 - 8 + 10 + 12 - .... + 60
B =
2)
a) \(x\in\left\{2;1;0;-1;-2\right\}\)
b) \(x\in\left\{6;-6;5;-5;4\right\}\)
c) \(x\in\left\{-9;-11;-10\right\}\)
3)
\(\left(a;b\right)\in\left\{\left(0;1\right);\left(0;-1\right);\left(1;0\right);\left(-1;0\right)\right\}\)

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Bài 7:
a, \(x\) = \(\dfrac{1}{5}\) + \(\dfrac{2}{11}\)
\(x\) = \(\dfrac{11}{55}\) + \(\dfrac{10}{55}\)
\(x=\dfrac{21}{55}\)
b, \(\dfrac{x}{15}\) = \(\dfrac{3}{5}\) - \(\dfrac{2}{3}\)
\(\dfrac{x}{15}\) = \(\dfrac{9}{15}\) - \(\dfrac{10}{15}\)
\(\dfrac{x}{15}\) = \(\dfrac{1}{15}\)
\(x\) = 1
c, \(\dfrac{11}{8}\) + \(\dfrac{13}{6}\)= \(\dfrac{85}{x}\)
\(\dfrac{33}{24}\) + \(\dfrac{52}{24}\) = \(\dfrac{85}{x}\)
\(\dfrac{85}{24}\) = \(\dfrac{85}{x}\)
24 = \(x\)

a) Ta có:
(a - b) ⋮ 6
12b ⋮ 6
⇒ [(a - b) + 12b] ⋮ 6
⇒ (a - b + 12b) ⋮ 6
⇒ (a + 11b) ⋮ 6
b) Ta có:
(a + 11b) ⋮ 6 (cmt)
12a ⋮ 6
12b ⋮ 6
⇒ [12a + 12b - (a + 11b)] ⋮ 6
⇒ (12a + 12b - a - 11b) ⋮ 6
⇒ (11a + b) ⋮ 6

III
1 It's colder today than yesterday
2 It takes 4 hours to travel by car and fives hours by train
3 We were busier at work today than everyday
4 Jane's sister cooks worse than her
5 Nobody in this team can play football as well as Tom
IV
1 D
2 A





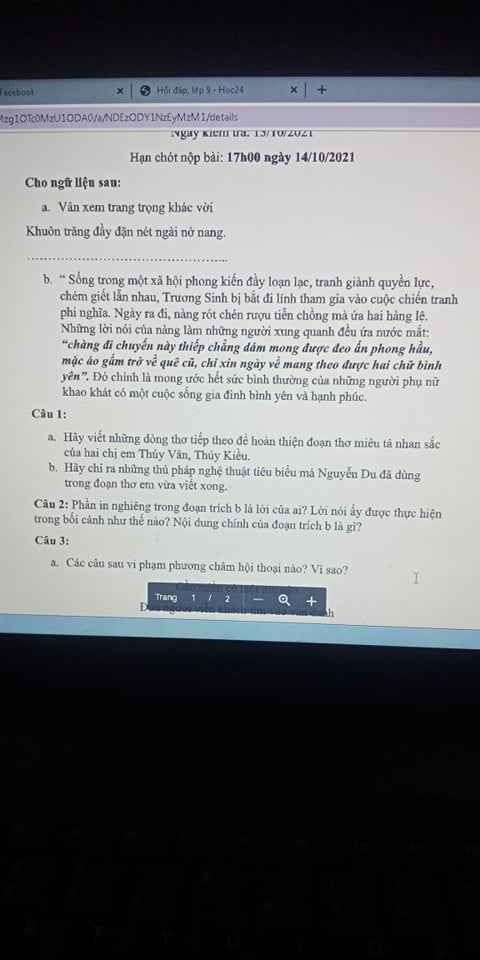 mọi người giúp mình bài này với câu 1 với câu 2 thôi
mọi người giúp mình bài này với câu 1 với câu 2 thôi
a: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-55^0=35^0\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(BC=\dfrac{16}{sin55}\simeq19,53\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{BC^2-AB^2}\simeq11,2\left(cm\right)\)
b: ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\) và \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: XétΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC;AC^2=CH\cdot BC\); \(AH^2=HB\cdot HC;AB\cdot AC=BC\cdot HA\)
\(BM\cdot CN\cdot BC\)
\(=\dfrac{CH^2}{CA}\cdot\dfrac{BH^2}{BA}\cdot BC\)
\(=\dfrac{AH^4}{AC\cdot AB}\cdot BC\)
\(=\dfrac{AH^4}{AH\cdot BC}\cdot BC=AH^3\)