phương trình dao động điều hòa của chất điểm có khối lượng 500g dao động điều hòa \(x=10cos\left(\pi t+\dfrac{\pi}{3}\right)\)cm/s. Viết biểu thức tính động năng và thế năng biến thiên theo thời gian
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
30 tháng 12 2020
Ok cần thì tui làm cho
Trước tiên cậu cần phải biết biểu thức của thế năng
\(W_t=\dfrac{1}{2}kx^2\)
Thay phương trình x đã cho vô:
\(W_t=\dfrac{1}{2}k.A^2.\cos^2\left(2\pi t+\dfrac{2\pi}{3}\right)\)
\(\cos^2\left(2\pi t+\dfrac{2\pi}{3}\right)=\dfrac{\cos4\left(\pi t+\dfrac{2\pi}{3}\right)+1}{2}\)
\(\Rightarrow W_t=\dfrac{1}{4}kA^2.\left[\cos4\left(\pi t+\dfrac{2\pi}{3}\right)+1\right]\)
Nhìn vào biểu thức ta kết luận được thế năng trong dao động của con lắc lò xo biến thiên tuần hoàn với chu kỳ là \(T=\dfrac{2\pi}{4\pi}=\dfrac{1}{2}\left(s\right)\)
Tương tự với động năng, ta sử dụng công thức không thời gian:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Rightarrow v^2=\omega^2\left(A^2-x^2\right)\)
\(\omega^2=\dfrac{k}{m}\Rightarrow m=\dfrac{k}{\omega^2}\)
\(\Rightarrow W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}.\dfrac{k}{\omega^2}.\omega^2\left(A^2-x^2\right)=\dfrac{1}{2}kA^2\left(1-\cos^2\left(2\pi t+\dfrac{2\pi}{3}\right)\right)\)
\(=\dfrac{1}{2}kA^2\left(1-\dfrac{\cos4\left(\pi t+\dfrac{2\pi}{3}\right)+1}{2}\right)=\dfrac{1}{4}kA^2\left[1-\cos4\left(\pi t+\dfrac{2\pi}{3}\right)\right]\)
Vậy động năng biến thiên tuần hoàn với chu kỳ là: \(T=\dfrac{2\pi}{4\pi}=\dfrac{1}{2}\left(s\right)\)
Nếu như ko sử dụng công thức ko thời gian, cậu có thể đạo hàm phương trình x ra, sẽ ra phương trình vận tốc và biến đổi là xong
\(v=x'=-\omega A\sin\left(\omega t+\varphi\right)=-2\pi.A\sin\left(2\pi t+\dfrac{2\pi}{3}\right)\)
HT
28 tháng 12 2020
Dạo này chả muốn làm Lý gì nên lười ghé box Lý lắm :( Cậu còn cần ko?
20 tháng 8 2023
2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
30 tháng 9
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi
HT
30 tháng 12 2020
\(A^2=A_1^2+A^2_2+2A_1A_1\cos\left(\widehat{A_1A_1}\right)\Rightarrow\left(\widehat{A_1A_2}\right)=\dfrac{\pi}{2}\)
Chỗ này đề bài ko cho rõ thì chia làm 2 trường hợp, x1 nhanh pha hơn hoặc x2 nhanh pha hơn, rồi tính được phi 2
Bấm máy là xong luôn pha ban đầu của dao động tổng hợp, biết bấm ko để tui chỉ luôn?
Thôi chỉ luôn đi, mất công hỏi nhiều mệt người
SHIFT Mode , cái nút tròn ở giữa ấy, ấn phía bên dưới, rồi nhấn 3, rồi nhấn tiếp 2
Nhấn tiếp Mode, rồi nhấn số 2
Nhấn SHIFT Mode lần nữa, rồi nhấn số 4 để nó chuyển về radian
Nhập theo mẫu sau: A1 SHIFT (-) phi 1 +A2 SHIFT (-) phi 2 , rồi nhất "=",nó sẽ ra kết ủa y hệt cái phương trình đã cho, từ đó tìm được pha ban đầu của phương trình tổng hợp. Biết phi 2, biết phi, dễ dàng tính được biểu thức
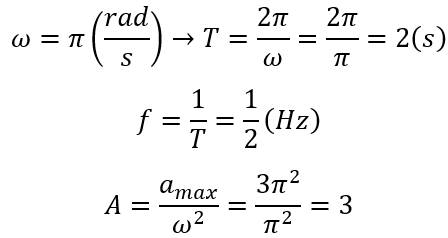
Biểu thức động năng biến thiên theo thời gian:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\omega^2A^2sin^2\left(\omega t+\varphi\right)\)
\(\Rightarrow W_đ=\dfrac{1}{2}\cdot0,5\cdot0,1^2\cdot sin^2\left(\pi t+\dfrac{\pi}{3}\right)=0,0025sin^2\left(\pi t+\dfrac{\pi}{3}\right)\left(J\right)\)
Biểu thức thế năng biến thiên theo thời gian:
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}kA^2cos^2\left(\omega t+\varphi\right)\)
\(\Rightarrow W_t=\dfrac{1}{2}\cdot m\omega^2A^2cos^2\left(\omega t+\varphi\right)=0,025cos^2\left(\pi t+\dfrac{\pi}{3}\right)\left(J\right)\)