Bài 5 Cho x, y là các số thực thỏa mãn x^2 + y^2 + xy 3x 3y + 3=0. Chứng minh biểu thức P = (3x +2y 6)^1010 + ( xy+1)^1011 + 2021 có giá trị là một số nguyên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
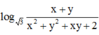
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
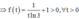
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 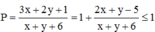
vì 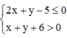
Vậy Pmax = 1 khi và chỉ khi 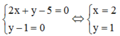

Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
![]()
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
![]()
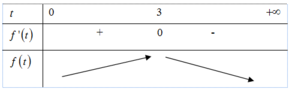
![]()
![]()
Khi đó, 
vì 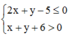
Vậy Pmax = 1 khi và chỉ khi 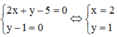

Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Cho x, y, z là các số thực dương thỏa mãn đẳng thức xy yz zx=5. Tìm GTNN của biểu thức \(P=\frac{3x 3y 2z}{\sqrt{6\left(... - Hoc24
mình cảm ơn bạn nhiều ạ <3 bạn có thể giúp mình mấy câu mình vừa đăng không

Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
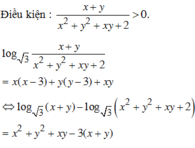
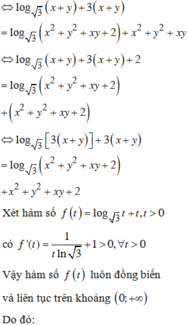
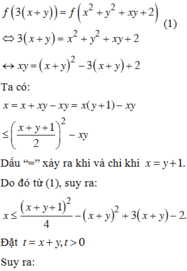
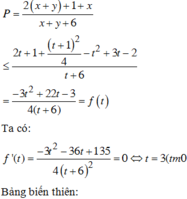



\(P=\sqrt{\frac{1}{36}\left(11a+7b\right)^2+\frac{59\left(a-b\right)^2}{36}}+\sqrt{\frac{1}{36}\left(7a+11b\right)+\frac{59\left(a-b\right)^2}{36}}\)
\(=\sqrt{\frac{1}{16}\left(3a+5b\right)^2+\frac{5\left(a-b\right)^2}{16}}+\sqrt{\frac{1}{16}\left(5a+3b\right)^2+\frac{5\left(a-b\right)^2}{16}}\)
\(\ge\frac{1}{6}\left(11a+7b\right)+\frac{1}{6}\left(7a+11b\right)+\frac{1}{4}\left(3a+5b\right)+\frac{1}{4}\left(5a+3b\right)\)
\(=5\left(a+b\right)=5.2016=10080\)

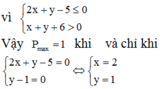

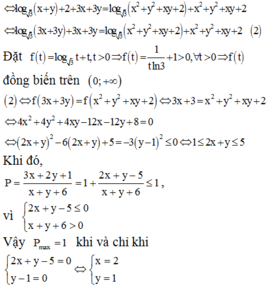
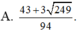
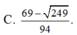
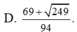
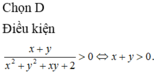

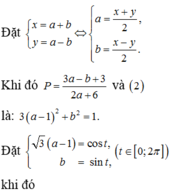




Mình tự làm tận 1h nên hơi dài 1 tí nhưng chắc chắn đúng đó :))
Ta có: x2 + y2 + xy .- 3x - 3y + 3 = 0
=>( x2 - 2x + 1) - x + ( y2 - 2y + 1) - y + xy + 1 = 0
=> (x-1)2 + (y-1)2 + ( -x + -y + xy +1) = 0
=> (x-1)2 + (y-1)2 + [(-x+ xy) + (-y+1)] = 0
=> (x-1)2 + (y-1)2 + [ x(y-1) - (y-1)] = 0
=> (x-1)2 + (y-1)2 + (x-1)(y-1) = 0
=> (x-1)2 + 2.1/2.(x-1)(y-1) + (1/2)2.(y-1)2 + 3/4.(y-1)2 = 0
=> [x-1+1/2(y-1) ]2 + 3/4.(y-1)2 = 0
Vì: [x-1+1/2(y-1) ]2 >= 0 với mọi x;y thuộc R
3/4.(y-1)2 >= 0 với mọi y thuộc R
=> (x-1+1/2y -1/2 = 0) và ( y-1 = 0)
=> (x = 1/2 -1/2y+1) và (y=1)
=> x = y =1
Chỗ này thay giá trị vào biểu thức rồi chứng minh = cách chỉ ra các cơ số của từng lũy thừa là số nguyên là xong.
đúng đó