cho hình chóp S.ABC gọi M,N lần lượt là trung điểm SB, AB. Trên cạnh BC lấy điểm P sao cho P không phải là trung điểm BC
a) Tìm giao tuyến
1. (MNP) giao (SAB)
2. (MNP) giao (SBC)
3. (MNP) giao (ABC)
b) chứng minh MN ll (SAC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 7 2017
Chọn A.
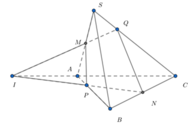
Phương pháp : Dựng điểm Q và áp dụng định lý Menenaus.
Cách giải : Gọi I là giao điểm của PN và AC. Suy ra Q là giao điểm của IM và SC.
Áp dụng định lý Menenaus cho tam giác SAC ta có :
CM
17 tháng 1 2018
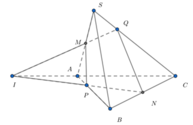
Chọn đáp án A
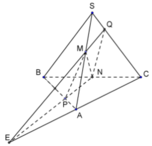
Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
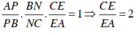
Áp dụng định lý Menelaus vào tam giác SAC ta có:
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2021
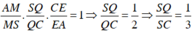
Trong mp (ABCD), nối MN kéo dài lần lượt cắt AB và AD kéo dài tại E và F
Trong mp (SAB), nối PE cắt SA tại G \(\Rightarrow PG=\left(MNP\right)\cap\left(SAB\right)\)
Trong mp (SAD), nối PF cắt SD tại H \(\Rightarrow PH=\left(MNP\right)\cap\left(SAD\right)\)
\(NH=\left(MNP\right)\cap\left(SCD\right)\)
\(GM=\left(MNP\right)\cap\left(SBC\right)\)
a:
1: \(M\in SB\subset\left(SAB\right)\)
\(M\in\left(MNP\right)\)
Do đó: \(M\in\left(SAB\right)\cap\left(MNP\right)\)(1)
\(N\in AB\subset\left(SAB\right)\)
\(N\in\left(MNP\right)\)
Do đó: \(N\in\left(SAB\right)\cap\left(MNP\right)\left(2\right)\)
Từ (1),(2) suy ra \(\left(SAB\right)\cap\left(MNP\right)=MN\)
2:
\(M\in SB\subset\left(SBC\right);M\in\left(MNP\right)\)
=>\(M\in\left(SBC\right)\cap\left(MNP\right)\)(3)
\(P\in BC\subset\left(SBC\right);P\in\left(MNP\right)\)
=>\(P\in\left(SBC\right)\cap\left(MNP\right)\)(4)
Từ (3),(4) suy ra \(\left(SBC\right)\cap\left(MNP\right)=MP\)
3:
\(N\in AB\subset\left(ABC\right);N\in\left(MNP\right)\)
=>\(N\in\left(ABC\right)\cap\left(MNP\right)\)(5)
\(P\in BC\subset\left(ABC\right);P\in\left(MNP\right)\)
=>\(P\in\left(ABC\right)\cap\left(MNP\right)\left(6\right)\)
Từ (5),(6) suy ra \(\left(ABC\right)\cap\left(MNP\right)=NP\)
b: Xét ΔBAS có BN/BA=BM/BS
nên NM//AS
=>MN//(SAC)