Tính giá trị biểu thức
A=5x(4x2-2x+1)-2x\(\subset\)10x2-5x-2\(\supset\)với x=15
MỌI NGƯỜI GIÚP K NHA MK ĐANG CẦN GẤP ,AI NHANH MK TÍCH 2 CÁI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2017
P = 5x ( 4x2 - 2x + 1 ) - 2x ( 10x2 - 5x - 2 )
P = 20x3 - 10x2 + 5x - 20x3 + 10x2 + 4x
P = 5 x + 4x = 9x
Thay x vào biểu thúc ta có :
9 . 15 = 135
Vậy giá trị của biểu thức là 135 khi x = 15
UB
1
TA
20 tháng 7 2021
`5x(4x^2-2x+1)-2x(10x^2-5x-2)`
`= 20x^3-10x^2+5x - (20x^3-10x^2-4x)`
`=9x`
Thay `x=15` có: `9.15=135`.
4 tháng 8 2017
E = x^2 + x + 1
E = (x^2 + 2x.\(\frac{1}{2}\)+1/4 ) + 3/4
E = (x+ 1/4 )^2 + 3/4
Do ...... ( đến đây bn tự làm nha)
H = ( x-1)^2 + ( x-7)^2
H = x^2 - 2x + 1 + x^2 - 14x + 49
H = 2x^2 - 16x + 50
H = [\(\left(\sqrt{2}x\right)^2-2.\sqrt{2}x.\frac{16}{2.\sqrt{2}}+32\)] + 18
H = ( \(\sqrt{2}x-\frac{16}{2\sqrt{2}}\))2 + 18
.....
D = x^2 -20x + 101
D =( x^2 - 2.x.10 + 100) + 1
D = (x-10) ^2 + 1
....
G = x^2 + 10x + 26 + y^2 + 2y + 2020
G = ( x^2 + 10x + 25) + (y^2+2y+1) + 2020
G = (x+5)^2 + ( y+1)^2 + 2020
....
Có gì ko hiểu hỏi mik
4 tháng 8 2017
E=X2+2.X.1/2 + (1/2)2-(1/2)2+1
E=(X+1/2)2+3/4 >=3/4
vậy MIN E=3/4 khi x=-1/2
các câu khác phân tích tương tự
NT
2
PD
15 tháng 7 2021
$D\,=2x(10x^2-5x-2)-5x(4x^2-2x-1)\\\quad =20x^3-10x^2-4x-20x^3+10x^2+5x\\\quad =(20x^3-20x^3)+(-10x^2+10x^2)+(-4x+5x)\\\quad =x$
Thay $x=-5$ vào $D=x$
$\Rightarrow D=-5$
Vậy $D=-5$ với $x=-5$
15 tháng 7 2021
Ta có: \(D=2x\left(10x^2-5x-2\right)-5x\left(4x^2-2x-1\right)\)
\(=20x^3-10x^2-4x-20x^2+10x^2+5x\)
=x=-5
8 tháng 8 2018
\(\left|x\right|=2\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}}\)
Khi x = 2 thì \(5x^2-2x+3x-1=5.2^2-2.2+3.2-1=20-4+6-1=21\)
Khi x = -2 thì \(5x^2-2x+3x-1=5.\left(-2\right)^2-2.\left(-2\right)+3.\left(-2\right)-1\)
\(=20+4-6-1=17\)
4 tháng 8 2017
Chả bik x- y= 5 có phải trong đề ko, giờ giải x+y = 3 trước
Ta có x2+y2 + 2xy - 4x - 4y + 1 = (x2+ 2xy + y2) - 4 ( x+y) + 1 = (x+y)^2 - 4(x+y) + 1 (1)
Thay x+y = 3 vào 1, có:
3^2 - 4.3 + 1 = 9-12 + 1 = -2
Vậy GTBT x2+y2 + 2xy - 4x - 4y + 1 vs x+ y = 3 là -2
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
\(\begin{array}{l}a){\rm{ }}3{x^2}-{\rm{ }}3x\left( {x{\rm{ }}-{\rm{ }}2} \right){\rm{ }} = {\rm{ }}36\\ \Leftrightarrow 3{x^2}-{\rm{ [}}3x.x + 3x.( - 2)] = 36\\ \Leftrightarrow 3{x^2} - (3{x^2} - 6x) = 36\\ \Leftrightarrow 3{x^2} - 3{x^2} + 6x = 36\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 36:6\\ \Leftrightarrow x = 6\end{array}\)
Vậy x = 6
\(\begin{array}{l}b){\rm{ }}5x\left( {4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}2x\left( {10{x^2}-{\rm{ }}5x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }} - 36\\ \Leftrightarrow 5x.4{x^2} + 5x.( - 2x) + 5x.1 - [2x.10{x^2} + 2x.( - 5x) + 2x.2] = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - (20{x^3} - 10{x^2} + 4x) = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - 20{x^3} + 10{x^2} - 4x = - 36\\ \Leftrightarrow (20{x^3} - 20{x^3}) + ( - 10{x^2} + 10{x^2}) + (5x - 4x) = - 36\\ \Leftrightarrow x = - 36\end{array}\)
Vậy x = -36
CM
1 tháng 7 2019
Điều kiện xác định của phân thức: x ≠ -10, x ≠ 10
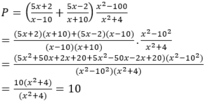
Vậy giá trị P =10 với mọi x ≠ ± 10
\(A=5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x-2\right)\)
\(=20x^3-10x^2+5x-20x^3+10x^2+4x\)
\(=9x=9.15=135\)