Các khẳng định sau đúng hay sai? Vì sao?
a) 6 \( \in \) ƯC(24, 30); b) 6 \( \in \) ƯC(28,42);
c) 6 \( \in \) ƯC(18, 24, 42).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sai vì 8 không là ước chung của 12 và 24
Sửa lại:
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
=> ƯC(12, 24) = {1; 2; 3; 4; 6; 12}
b) Đúng.
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(48) = {1; 2; 3; 4; 6; 12; 24; 48}
=> ƯC(36, 12, 48) = {1; 2; 3; 4; 6; 12}.

a, Sai
Sửa: \(ƯC\left(12,24\right)=\left\{1;2;3;4;6;12\right\}\)

Ta có: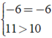 ⇒ VT = 11 + ( - 6 ) > VP = 10 + ( - 6 )
⇒ VT = 11 + ( - 6 ) > VP = 10 + ( - 6 )
Khẳng định trên là sai.

Ta có: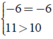 ⇒ VT = 11 + ( - 6 ) > VP = 10 + ( - 6 )
⇒ VT = 11 + ( - 6 ) > VP = 10 + ( - 6 )
Khẳng định trên là sai.

- 8 ∈ ƯC(16, 40) là đúng vì 16 chia hết cho 8 và 40 cũng chia hết cho 8
- 8 ∈ ƯC(32, 28) là sai vì 32 chia hết cho 8 nhưng 28 không chia hết cho 8

Ta có: -6 < -5
⇒ (-6).5 < (-5).5 (Nhân cả hai vế với 5 > 0 được BĐT cùng chiều).
⇒ Khẳng định đúng.

Ta có: VP = 5 - 10 = - 5
Mà - 5 > - 6 ⇒ VP > VT.
Vậy khẳng định trên là sai.

Ta có: VP = 5 - 10 = - 5
Mà - 5 > - 6 ⇒ VP > VT.
Vậy khẳng định trên là sai.

-6 < -5
⇒ (-6).(-3) > (-5).(-3) (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).
⇒ Khẳng định sai.
a) Đúng
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
=> ƯC(24,30) = {1; 2; 3; 6).
Vậy 6 \( \in \) ƯC(24, 30)
b) Sai
Ư(28) = {1; 2; 4; 7; 14; 28}
Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
=> ƯC(28,42) = {1; 2; 7; 14}.
Vậy 6 \( \notin \) ƯC(28,42)
c) Đúng
Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
=> ƯC(18, 24, 42} = {1; 2; 3; 6).
Vậy 6 \( \in \) ƯC(18, 24, 42)