Biểu đồ tranh sau đây cho biết số lượt ô tô vào gửi tại một bãi đỗ xe vào các ngày trong một tuần.
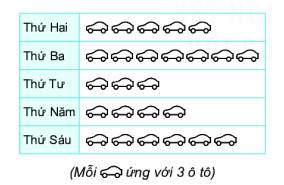
Hãy lập bảng thống kê biểu diễn số ô tô vào gửi tại bãi đỗ xe ở các ngày trong tuần.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xe gửi số giờ là: 2h30`- 9h15`=6h45`=6,75h
Xe gửi giờ đầu phải trả 15000đ vậy soos giờ còn lại xe gửi tiếp là: 6,75h-1h=5,75h
Mỗi giờ sau phải trả 10000đ ; Sau giờ thứ nhất thì xe gửi phải trả số tiền là:
5,75.10000=57500đ
Vậy tất cả xe phải trả số tiền là:
57500+15000=72500 đ

4 xe ô tô và 4 xe máy vì 4 ô tô là 16 bánh và 4 xe máy là 8 bánh và tổng là 24 bánh

các bạn làm ơn giúp mình đi mà gần phải nộp rồi hu hu ai xong trước mình tích cho các bạn nhớ làm theo phương pháp giả thiết tạm và giải chi tiết hộ mình nhé.

Bài giải
Số xe máy trong bãi đỗ xe là :
1206 : 3 = 402 ( xe )
Bãi đỗ xe đó có số xe ô tô là :
1206 - 402 = 804 ( xe )
Đáp số : 804 xe ô tô
Chúc bạn học tốt !!!

Phân số chỉ số xe ô tô ở bãi đỗ xe là:
\(1-\frac{1}{3}=\frac{2}{3}\)
Bãi đỗ xe đó có số ô tô là:
1206:2/3=804 (xe )

a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
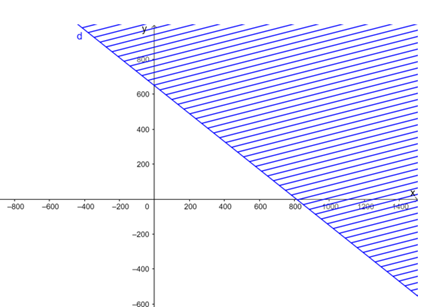
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
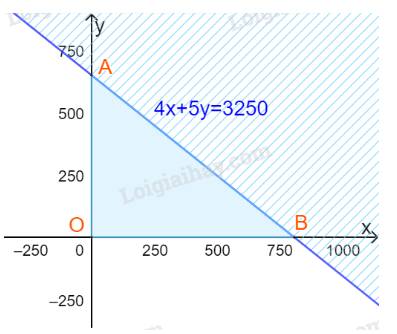
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.
Số ô tô vào gửi ngày
Thứ hai là: 5.3=15 (xe)
Thứ ba là: 7.3=21 (xe)
Thứ tư là: 3.3=9 (xe)
Thứ năm là: 4.3=12 (xe)
Thứ sáu là: 6.3=18 (xe)
Thứ
Hai
Ba
Tư
Năm
Sáu
Số ô tô
15
21
9
12
18