1) Tính số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu.
2) Hãy viết mỗi số tự nhiên sau thành tổng giá trị các chữ số của nó bằng cách dùng các luỹ thừa của 10 theo mẫu:
4 257 = 4 . 103 +2. 102 + 5.10 + 7.
a) 23 197
b) 203 184.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(23197=2\cdot10^4+3\cdot10^3+10^2+9\cdot10^1+7\)
b) \(203184=2\cdot10^5+3\cdot10^3+10^2+8\cdot10^1+4\)

Tham khảo:
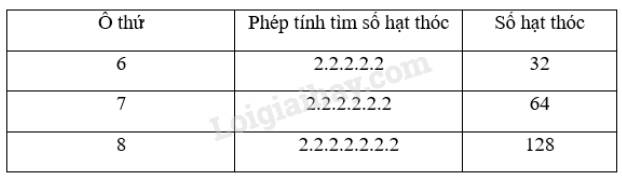
Để tìm số hạt thóc ở ô số 8, ta phải thực hiện phép nhân có 7 thừa số 2.

\(215=2\cdot10^2+1\cdot10+5\cdot10^0\)
\(902=9\cdot10^2+2\cdot10^0\)
\(2020=2\cdot10^3+2\cdot10\)
\(883011=8\cdot10^5+8\cdot10^4+3\cdot10^3+10+1\cdot10^0\)

\(215 = 2. 10^2 + 1. 10^1 + 5. 10^0\)
\(902 = 9.10^2 + 0.10^1+ 2 . 10^0\)
\(2 020 = 2.10^3+0.10^2+2.10^1+0. 10^0\)
\(883 001 = 8.10^5+8.10^4+3.10^3+0.10^2+0.10^1+1. 10^0\)

Gọi tổng số hạt thóc là A thì ta có phép tính:
\(A=1+2+2^2+2^3+...+2^{31}\)
\(\Rightarrow2A=2+2^2+2^3+2^4...+2^{32}\)
\(\Rightarrow2A-A=\left(2+2^2+2^3+2^4...+2^{32}\right)-\left(1+2+2^2+2^3+...+2^{31}\right)\)
\(\Rightarrow A=2^{32}-1\)
\(\Rightarrow A=\text{4 294 967 296}-1=\text{4 294 967 295}\)

Theo điều kiện của bài : đặt 1 hạt thóc vào ô thứ nhất . 2 hạt thóc vào ô thứ hai. Các ô tiếp theo cú thế nhân đôi.
Ta có:
1.1+2.2+3.2+4.2+....+64.2
=1+2.(2+3+4+...+64)
=1+2.2079
=1+4158
=4159
Chẳng biết có đúng không nữa ? Đúng hay sai xin ibox cho mình nhé!
1. Số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu:
2.2.2.2.2.2 = 26 = 64
2. a) 23 197 = 2.104 + 3.103 + 1.102 + 9.101 + 7
b) 203 184 = 2.105 + 0.104 + 3.103 + 1.102 + 8.101 + 4