Cho parabol có phương trình \({y^2} = 8x\). Tìm tiêu điểm và đường chuẩn của parabol.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Từ phương trình chính tắc \({y^2} = 12x\) ta có \(p = 6\)
Suy ra
+) Tiêu điểm của parabol \(F(3;0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + 3 = 0\)
b) Từ phương trình chính tắc \({y^2} = x\) ta có \(p = \frac{1}{2}\)
Suy ra
+) Tiêu điểm của parabol \(F(\frac{1}{4};0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + \frac{1}{4} = 0\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Ta có:
\(2p = \;\frac{5}{2} \Rightarrow p = \frac{5}{4} \Rightarrow \frac{p}{2} = \frac{5}{8}\).
Tiêu điểm của parabol là: \(F\left( {\frac{5}{8};0} \right)\)
Phương trình đường chuẩn là: \(x + \frac{5}{8} = 0\)
b) Ta có:
\(2p = 2\sqrt 2 \Rightarrow p = \sqrt 2 \Rightarrow \frac{p}{2} = \frac{{\sqrt 2 }}{2}\).
Tiêu điểm của parabol là: \(F(\frac{{\sqrt 2 }}{2};0)\)
Phương trình đường chuẩn là: \(x + \frac{{\sqrt 2 }}{2} = 0\)
DH
0
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Tiêu điểm có tọa độ \((4;0)\) nên ta có \(p = 8\)
Suy ra phương trình chính tắc của parabol là: \({y^2} = 16x\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\), nên ta có \(p = - \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol có dạng \({y^2} = - \frac{2}{3}x\)
c) Gọi phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm \((1;4)\) vào phương trình \({y^2} = 2px\) ta có:
\({4^2} = 2p.1 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
d) Gọi \(F\left( {\frac{p}{2};0} \right)\), \(\Delta :x + \frac{p}{2} = 0\) lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:
\(d\left( {F,\Delta } \right) = \frac{{\left| {\frac{p}{2} + \frac{p}{2}} \right|}}{1} = 8 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
CM
13 tháng 9 2019
Đáp án: B.
Ta có khoảng cách từ tiêu điểm đến đường chuẩn của một parabol bằng p ⇒ p = 2
Vậy phương trình chính tắc của parabol là: y 2 = 2.2x ⇔ y 2 = 4x
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)
27 tháng 7 2023
a: PTHĐGĐ là:
x^2-3x+2=0
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
Khi x=2 thì y=2^2=4
Khi x=1 thì y=1^2=1
b: Δ=(2m+2)^2-4(2m-3)
=4m^2+8m+4-8m+12
=4m^2+16>0
=>Phương trình luôn có hai nghiệm
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
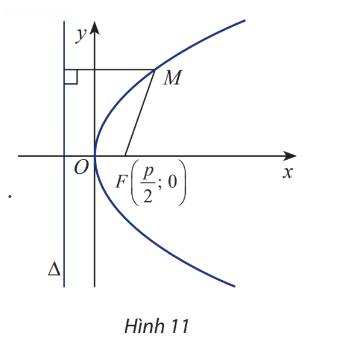
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)
Ta có: \(2p = 8 \Rightarrow p = 4\) nên (P) có tiêu điểm là \(F\left( {2;0} \right)\) và đường chuẩn là \(x = - 2\).