Hãy tự thiết kế một cổng chào hình parabol.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


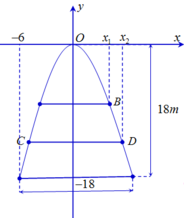
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m

Đáp án C
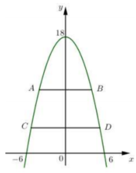


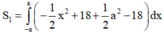



Diện tích hình phẳng giới hạn bởi parabol và đường thẳng CD là:

= − c 3 6 + c 3 2 − c 3 6 − c 3 2 = 2 c 3 3 S 1 = 2 3 S ⇒ 2 3 c 3 = 2 3 .144 = 96 ⇒ c = 2 18 3 ⇒ C D = 2 c ⇒ 4 18 3 ⇒ A B C D = 1 2 3

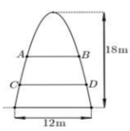
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
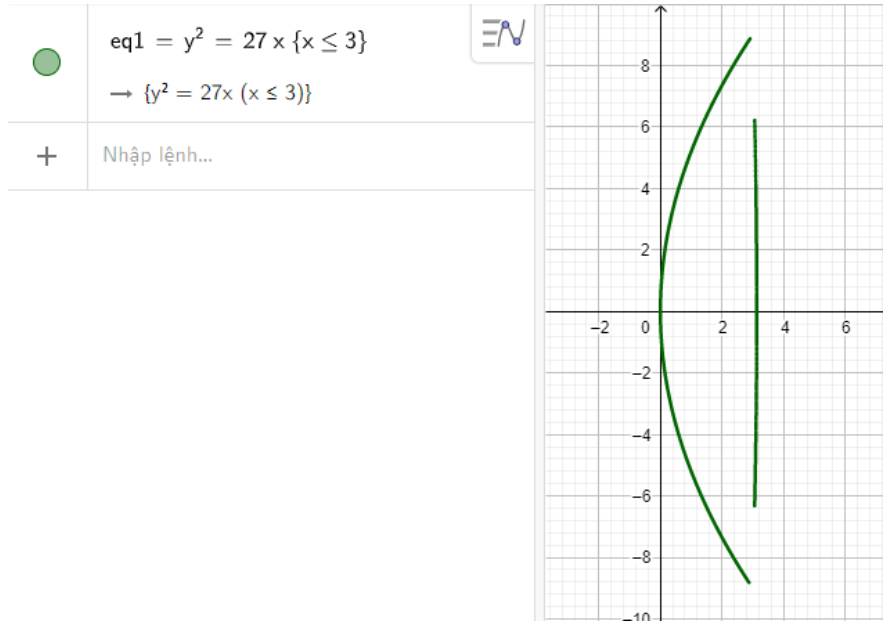
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
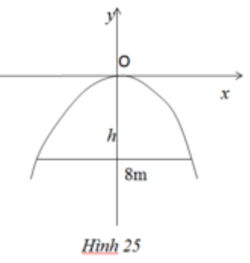
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:





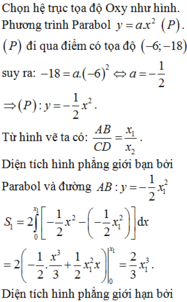
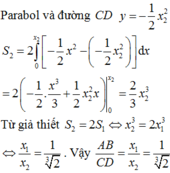

Khởi động phần mềm Geogebra và mở tính năng thanh trượt
Nhập các công thức y = ax^2 + bx + c , D = b^2 – 4ac vào vùng lệnh
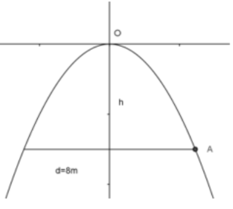
Điều chỉnh các thanh trượt ta có parabol như hình dưới
Ta được hình dạng của cổng chào hình parabol.