
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vẽ lại hình vẽ như dưới đây

Ta có \(AB = 18,x = 3 \Rightarrow A(3;9)\)
Gọi phương trình parabol tổng quát \({y^2} = 2px\)
Thay tọa độ điểm A vào phương trình ta có: \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Vậy phương trình parabol trên hệ trục tọa độ vừa chọn là \({y^2} = 27x\)
b) Từ câu a) ta có: \(p = \frac{{27}}{2}\)
Suy ra tiêu điểm của parabol là \(F\left( {\frac{{27}}{4};0} \right)\)
Vậy để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn \(\frac{{27}}{4}\) xentimét

Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\left( {p > 0} \right)\)
Vì \(AB = 40cm\) và \(h = 30cm\) nên \(A\left( {30;20} \right)\)
Do \(A\left( {30;20} \right)\) thuộc parabol nên ta có: \({20^2} = 2p.30 \Rightarrow p = \frac{{20}}{3}\)
Vậy parabol có phương trình chính tắc là: \({y^2} = \frac{{40}}{3}x\)

a) Chiều rộng của tấm bìa là \(\overline R = 170 \pm 2mm\), nghĩa là chiều rộng gần đúng \(R = 170\)với độ chính xác \(d = 2\)
Suy ra kích thước chiều rộng nằm trong khoảng \(\left[ {170 - 2;170 + 2} \right]\) hay \(\left[ {168;{\rm{ }}172} \right].\)
Tương tự, chiều dài của tấm bìa là \(\overline D = 240 \pm 2mm\)
Vậy kích thước chiều dài nằm trong khoảng \(\left[ {240 - 2;240 + 2} \right]\) hay \([238;242]\)
b) Chiều rộng gần đúng là 170 mm, chiều dài gần đúng là 240 mm.
Khi đó, diện tích tấm bìa là \(S = 170.240 = 40800\;(m{m^2})\)
Diện tích đúng, kí hiệu \(\overline S \), của tấm bìa trên thỏa mãn:
\(168.238 < \overline S < 172.242 \Leftrightarrow 39984 < \overline S < 41624\)
Do đó \(39984 - 40800 < \overline S - 40800 < 41624 - 40800\) hay \( - 816 < \overline S - S < 824 \Rightarrow \left| {\overline S - S} \right| < 824\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Cách 2:
Diện tích tấm bìa là:
\(\overline S = \left( {170 \pm 2} \right)\left( {240 \pm 2} \right) = 170.240 \pm \left( {170.2 + 240.2 + 2.2} \right) = 40800 \pm 824\left( {m{m^2}} \right)\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)

Khởi động phần mềm Geogebra và mở tính năng thanh trượt
Nhập các công thức y = ax^2 + bx + c , D = b^2 – 4ac vào vùng lệnh
Điều chỉnh các thanh trượt ta có parabol như hình dưới
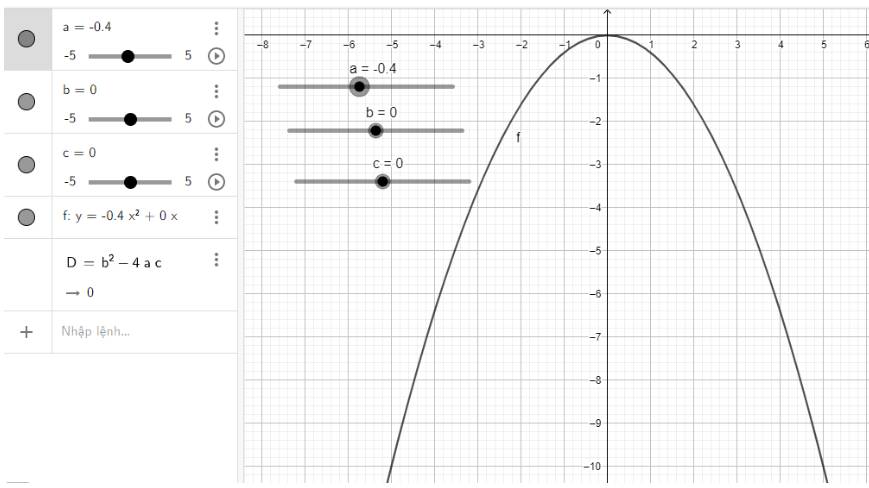
Ta được hình dạng của cổng chào hình parabol.

Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
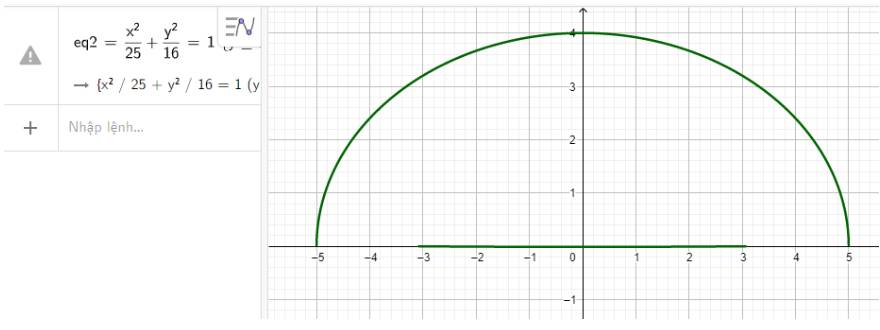
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên

Gọi \(y = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là thành cầu.
Chọn hệ trục tọa độ Oxy như hình dưới:
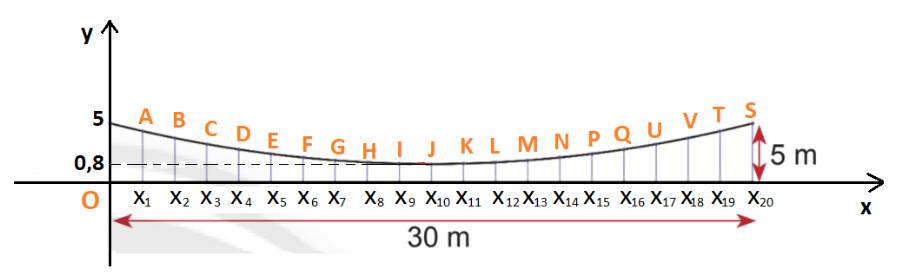
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.
Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.
Khoảng cách giữa hai dây cáp liền kề là: \(30:20 = 1,5\left( m \right)\)
Khi đó: \({x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;\)
Dễ thấy: các điểm có tọa độ (0; 5), (\({x_{10}};0,8\)), \(({x_{20}};5)\) thuộc đồ thị hàm số.
(Trong đó: \({x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.\))
Suy ra:
\(f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5\)
Và \(f(1) = a{.15^2} + b.15 + c = 0,8 \Leftrightarrow 225a + 15b + 5 = 0,8\)
\(f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5\)
Giải hệ phương trình \(\left\{ \begin{array}{l}225a + 15b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.\) ta được \(a = \frac{{7}}{{375}};b = - \frac{{14}}{{25}}\)
Như vậy \(y = \frac{{7}}{{375}}{x^2} - \frac{{14}}{{25}}x + 5\)
Gọi \({y_0},{y_1},{y_2},..{y_{20}}\) là tung độ của các điểm có hoành độ lần lượt là \({x_0},{x_1},{x_2},..{x_{20}}\)
Ta có:
\(\begin{array}{l}{y_0} = 5\\{y_1} = \frac{{7}}{{375}}.1,{5^2} - \frac{{14}}{{25}}.1,5 + 5\\{y_2} = \frac{{7}}{{375}}.{(2.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {2^2}.\frac{{7}}{{375}}.1,{5^2} - 2.\frac{{14}}{{25}}.1,5 + 5\\...\\{y_n} = \frac{{7}}{{375}}.{(n.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {n^2}.\frac{{7}}{{375}}.1,{5^2} - n.\frac{{14}}{{25}}.1,5 + 5\\ \Rightarrow T = {y_0} + {y_1} + {y_2} + .. + {y_{20}} = 5 + \frac{{7}}{{375}}.1,{5^2}.(1 + {2^2} + ... + {20^2}) - \frac{{14}}{{25}}.1,5.(1 + 2 + ... + 20) + 5.20\end{array}\)
Mà \(1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210\)
\( \Rightarrow T = 5 + \frac{{7}}{{375}}.1,{5^2}.2870 - \frac{{14}}{{25}}.1,5.210 + 5.20 \approx 49,14(m)\)
Do cần tính thêm 5% chiều dài để neo cố định và cần 2 thành mặt cầu nên tổng chiều dài của các dây cáp cần sử dụng là: \(49,14.2.105% = 103,2(m)\)
Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 103,2m.

15 cm = 0,15 m
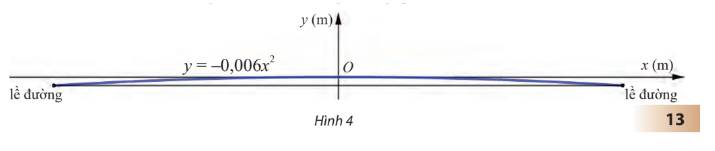
Tại vì gốc tọa độ đặt tại tim đường nên độ cao của lề đường so với tim đường là âm
Để tim đường cao hơn đường không quá 15 cm thì ta có bât phương trình sau:
\( - 0,006{x^2} \ge - 0,15 \Leftrightarrow 0,006{x^2} - 0,15 \ge 0\)
Xét tam thức bậc hai \(f\left( x \right) = 0,006{x^2} - 0,15\) có hai nghiệm phân biệt là \({x_1} = - 5;{x_2} = 5\) và \(a = 0,006 > 0\) nên \(f\left( x \right)\) dương khi x thuộc hai nửa khoảng \(\left( { - \infty ; - 5} \right];\left[ {5; + \infty } \right)\)
Vậy khi chiều rộng của đường lớn hơn 10 m thì tim đường cao hơn đường không quá 15 cm




Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới: