Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
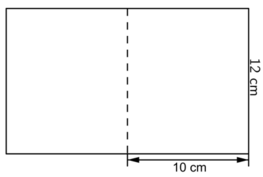
Chiều dài của cả tấm thiệp là:
10 x 2 = 20 (cm)
Diện tích tấm thiệp là:
12 x 20 = 240 (cm2)
Đáp số: 240 cm2
Cách 2:
Diện tích một nửa tấm thiệp là:
12 x 10 = 120 (cm2)
Diện tích cả tấm thiệp là:
120 x 2 = 240 (cm2).
Đáp số: 240 cm2.

Chiều rộng tấm thiệp là:
18:2=9(cm)
Diện tích tấm thiệp là:
18 nhân 9=162(cm)
Đáp số:162 cm

bài giải
chiều rộng tấm thiệp là :
14 : 2 = 7 (cm)
diện tích tấm thiệp là :
14 x 7 = 98 ( cm2 )
đáp số: 98 cm2
Chiều rộng của hình chữ nhật là:
14 : 2 = 7 ( cm )
Diện tích tam thiep là:
14 x 7 = 98 ( cm2 )
Đáp số: 98 cm2.

Gọi số tấm thiệp cần làm của lớp 7A,7B,7C lần lượt là a,b,c
Theo đề, ta có: a/15=b/14=c/11
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{15}=\dfrac{b}{14}=\dfrac{c}{11}=\dfrac{a+b+c}{15+14+11}=1\)
=>a=15; b=14;c=11

16/10 cách 27/11 41 ngày
20 000 - 15 000 = 5 000 đồng/ngày
5 000 * 41 = 205 000 đồng
như thế ko đủ
HT
từ 16 đến 27 là 11 ngày
số tiền Lan dành 1 ngày : 20000-15000 = 5 000 ( đồng )
số tiền Lan dành 11 ngày : 5000 x 11 = 55 000 ( đồng )
Số tiền cần có để mua giỏ hoa và tấm thiệp chúc mừng : 200 000 + 15 000 = 215 000 ( đồng )
Vậy Lan không đủ tiền mua hoa và thiệp để tặng mẹ
Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ vẽ không quá 30 giờ nên \(2x + 3y \le 30\)
- Số tấm thiệp tối thiểu là 12 tấm nên \(x + y \ge 12\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(A(6;6),\)\(B(15;0),\)\(C(12;0).\)
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: \(F = 10x + 20y\)
Tính giá trị của F tại các đỉnh của tam giác:
Tại \(A(6;6):\)\(F = 10.6 + 20.6 = 180\)
Tại \(B(15;0):\)\(F = 10.15 + 20.0 = 150\)
Tại \(C(12;0):\)\(F = 10.12 + 20.0 = 120\)
F đạt giá trị lớn nhất bằng 180 tại \(A(6;6).\)
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.