Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
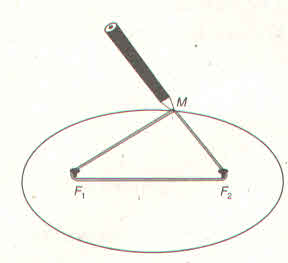
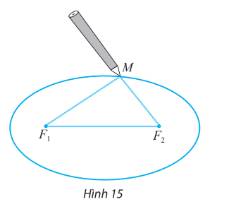
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 – 20√3
=> F2A = 20(2 – √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

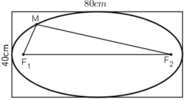
Giả sử Elip có phương trình 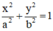
Độ dài trục lớn bằng 80cm ⇒ 2a = 80cm ⇒ a =40cm
Độ dài trục nhỏ bằng 40cm ⇒ 2b = 40cm ⇒ b = 20cm
Khi đó 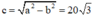 ⇒ F1F2 = 2c = 40√3 cm
⇒ F1F2 = 2c = 40√3 cm
Khoảng cách từ vị trí hai chiếc đinh F1, F2 đến hai mép là:
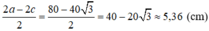
Độ dài vòng dây cuốn: MF1 + MF2 + F1F2 = 2a + 2c = 80 + 40√3 ≈ 149,3cm.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 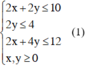
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
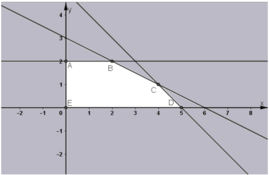
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 - 20√3
=> F2A = 20(2 - √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

a)
Nam ủng hộ x tờ tiền mệnh giá 20 nghìn đồng, tương ứng 20.x nghìn đồng
Và y tờ tiền mệnh giá 50 nghìn đồng, tương ứng 50.y nghìn đồng
Tổng số tiền ủng hộ là: \(20x + 50y\) (nghìn đồng)
b) Vì số tiền ủng hộ (\(20x + 50y\)nghìn đồng) phải nhỏ hơn hoặc bằng có tiền Nam có (700 nghìn đồng) nên ta có bất đẳng thức: \(20x + 50y \le 700\)

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
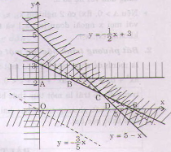
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

Từ giải thiết ta có: \(2a = 80 \Rightarrow a = 40,2b = 40 \Rightarrow b = 20\)
Suy ra, \(c = \sqrt {{a^2} - {b^2}} = 20\sqrt 3 \)
Suy ra vị trí đinh cách mép là \(a - c = 40 - 20\sqrt 3 = 5,36\) cm
Chiều dài vòng dây là \(2a + 2c = 2.40 + 2.20\sqrt 3 = 149,28\) cm
Vậy phải ghim hai cái đinh cách các mép tấm bìa 5,36 cm và lấy vòng dây có độ dài là 149,28 cm

Chọn C
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 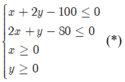
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
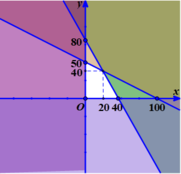
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 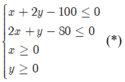
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ vẽ không quá 30 giờ nên \(2x + 3y \le 30\)
- Số tấm thiệp tối thiểu là 12 tấm nên \(x + y \ge 12\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(A(6;6),\)\(B(15;0),\)\(C(12;0).\)
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: \(F = 10x + 20y\)
Tính giá trị của F tại các đỉnh của tam giác:
Tại \(A(6;6):\)\(F = 10.6 + 20.6 = 180\)
Tại \(B(15;0):\)\(F = 10.15 + 20.0 = 150\)
Tại \(C(12;0):\)\(F = 10.12 + 20.0 = 120\)
F đạt giá trị lớn nhất bằng 180 tại \(A(6;6).\)
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.