Trên sông, một cano chuyển động thẳng đều theo hướng \(S{15^o}E\) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


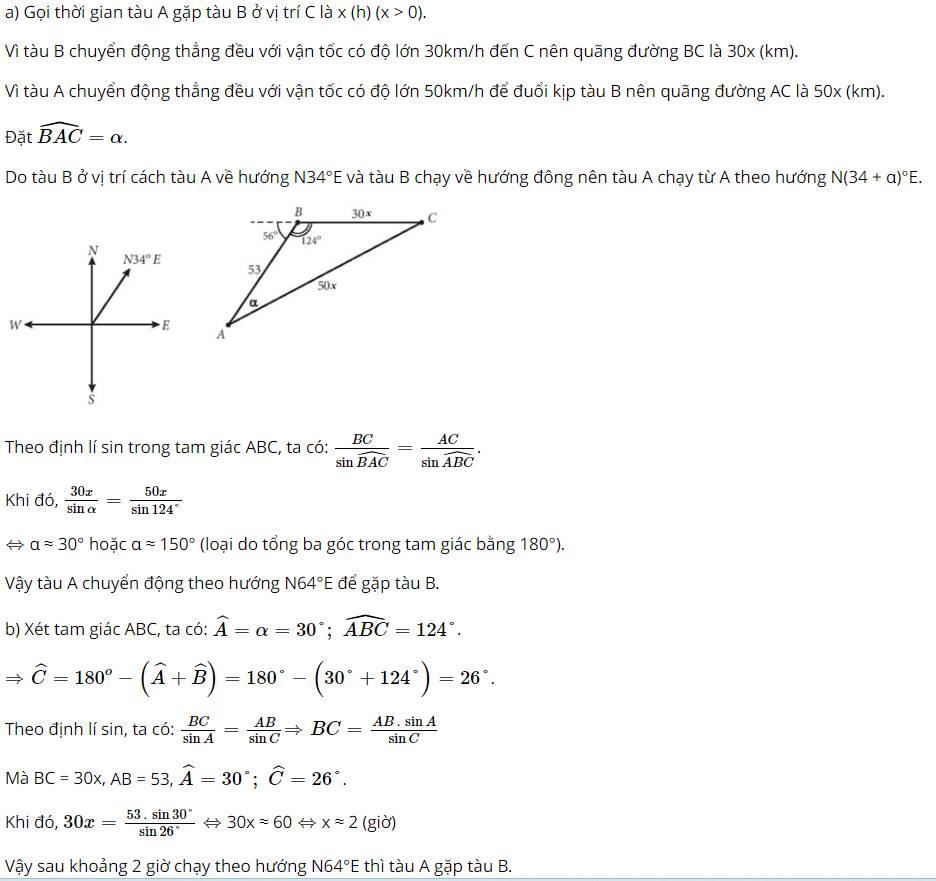
a)
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

Bài 1:
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x
⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625,
√∆’ = 25
x1 = 5 – 25 = -20,
x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Vậy Vận tốc của xuồng khi đi là 30 km/h
Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt nên :
4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt

Bài 1:Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
--Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
--khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
--Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt
nên : 4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt
tk nha

dòng sông chảy theo hướng A->B với \(v=2,5km/h\)
=> đây là vận tốc dòng nước
đổi \(1h30'=\dfrac{3}{2}h\)
\(=>v1=\dfrac{S}{t}=\dfrac{42}{\dfrac{3}{2}}=28km/h\)
mà ca nô đi từ A->B với vận tốc \(v1=28=vc+v=vc+2,5=>vc=v1-v=28-2,5\)\(=25,5km/h\)
đây là vận tốc thực ca nô
đi từ B->A \(=>v2=vc-2,5=25,5-2,5=23km/h\)
\(=>t1=\dfrac{S}{v2}=\dfrac{42}{23}\approx1,8h\)

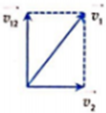
Gọi \(\overrightarrow{v_{12}},\overrightarrow{v_{23}}\) lần lượt là vận tốc của cano so với nước , của nước so với bờ
a. Khi cano chuyển động cùng chiều với dòng nước
\(v_{13}=v_{12}+v_{23}=60+15=75\left(km/h\right)\)
b. Khi cano chuyển động ngược chiều với dòng nước
\(v_{13}=v_{12}-v_{23}=60-15=45\left(km/h\right)\)
c. Khi cano chuyển động vuông góc với nước
\(v_{13}=\sqrt{v_{12}^2+v_{23}^2}=\sqrt{60^2+15^2}=15\sqrt{17}\approx62\left(km/h\right)\)
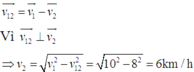
Tham khảo:
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.
Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} - {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} - 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h