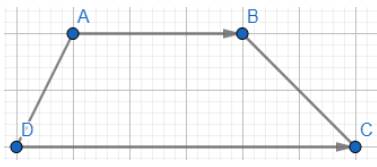
Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với \(\overrightarrow {AB} \)
b) Ngược hướng với \(\overrightarrow {AB} \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
BT
18 tháng 5 2017
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2019
\(\overrightarrow{u}=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{AD}=2\overrightarrow{AD}+\left(\overrightarrow{DC}+\overrightarrow{BA}\right)=2\overrightarrow{AD}\)\(\Rightarrow\overrightarrow{u}\) cùng hướng \(\overrightarrow{AD}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB.
Các vectơ cùng phương với vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {CD} \) và \(\overrightarrow {DC} \)
a) vectơ \(\overrightarrow {DC} \) cùng hướng với vectơ \(\overrightarrow {AB} \).
b) vectơ \(\overrightarrow {CD} \) ngược hướng với vectơ \(\overrightarrow {AB} \).