Cho hình chóp S.ABCD có đáy hình vuông tâm O và AB=a. Góc giữa SC và (SBD) bằng 30°, SA=SC, SB=SD. Thể tích khối chóp S.ABCD ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B

Ta có: S B A ^ = 60 ∘ ⇒ S A = A B tan 60 ∘ = a 3
V A . A C D = 1 3 S A . S A C D = 1 3 . a 3 . a 2 2 = a 3 3 6
Lại có: V S . A M N V S . A C D = S M S C . S N S D = 1 4 ⇒ V S . A M N = a 3 3 24

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
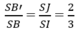
Do đó dễ thấy
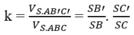

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

Đáp án A
Trong mặt phẳng dựng đường thẳng đi qua A và vuông góc vưới SB tại K
Ta chứng minh được
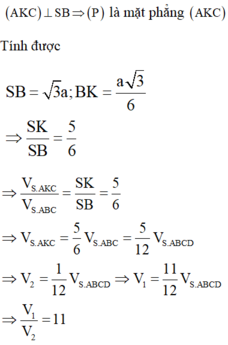
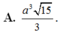
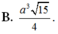
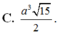
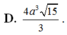
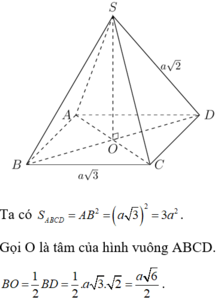
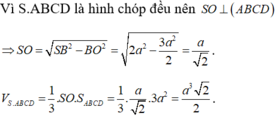

Vì `SA=SC; SB=SD`
Mà `O` là trung điểm `AC;BD`
`=>SO \bot AC; SO \bot BD`
`=>SO \bot (ABCD)`
Vì `OC \bot BD; OC \bot SO =>OC \bot (SBD)`
`=>(SC,(SBD))=\hat{OSC}=30^o`
Ta có: `OC=1/2 AC=\sqrt{2}/2 a`
`=>SO=[OC]/[tan \hat{OSC}]=\sqrt{6}/2 a`
`=>V_[S.ABCD]=1/3 . \sqrt{6}/2 a .a^2 = \sqrt{6}/6 a^3`.