a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
x | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(y = \tan x\) | ? | ? | ? | ? | ? |
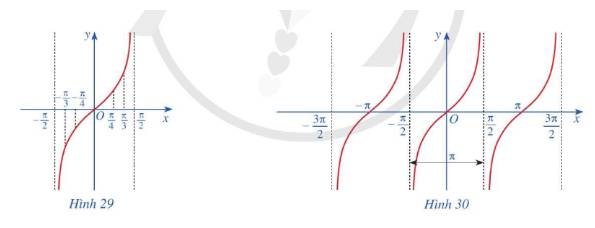
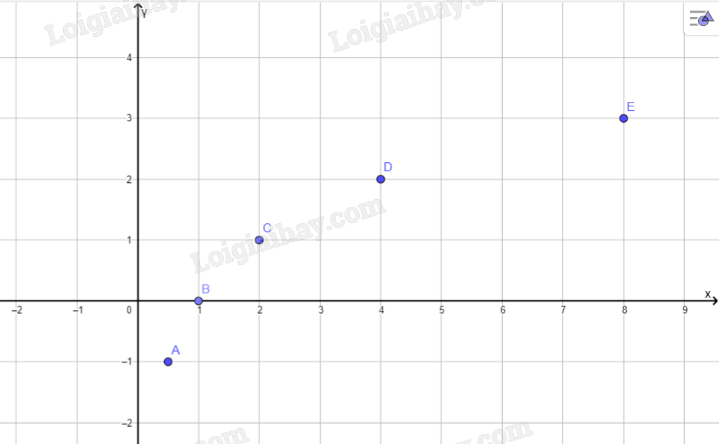
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; tanx) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) (Hình 29).
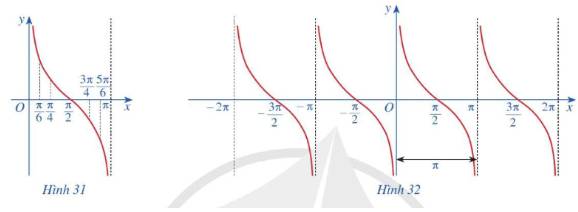
c) Làm tương tự như trên đối với các khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\),...ta có đồ thị hàm số \(y = \tan x\)trên D được biểu diễn ở Hình 30.








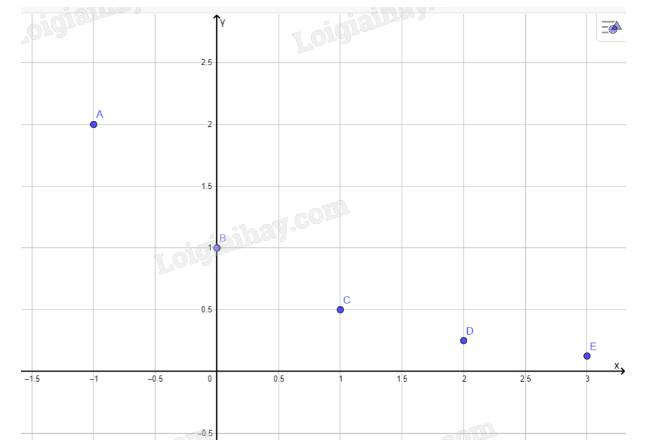

a)
x
\( - \frac{\pi }{3}\)
\( - \frac{\pi }{4}\)
0
\(\frac{\pi }{4}\)
\(\frac{\pi }{3}\)
\(y = \tan x\)
\( - \sqrt 3 \)
-1
0
1
\(\sqrt 3 \)
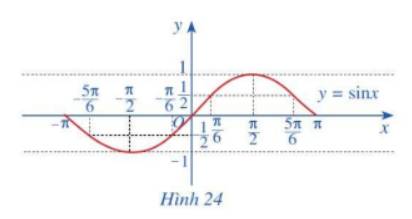
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; tanx) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) (Hình 29).
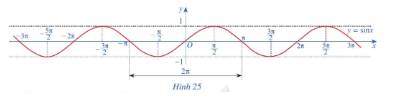
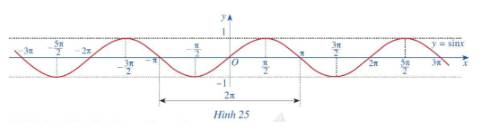
c) Làm tương tự như trên đối với các khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\),...ta có đồ thị hàm số \(y = \tan x\)trên D được biểu diễn ở Hình 30.