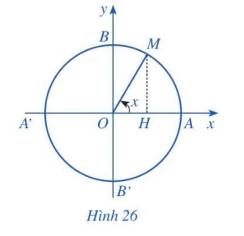
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = x\left( {rad} \right)\) (Hình 26). Hãy xác định \(\cos x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2023
a)
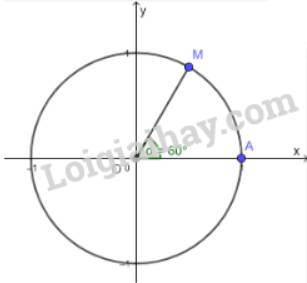
b) \(\cos 60^\circ \) bằng hoành độ của điểm M
\(\sin 60^\circ \) bằng tung độ của điểm M
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
21 tháng 9 2023
Tham khảo:
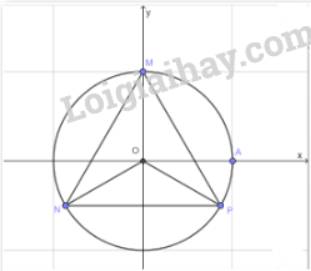
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.
Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất
Nên ta chỉ xác định duy nhất giá trị sint và cost.
b,
Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))
Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))
Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).
\(\cos x = \frac{{OH}}{{OM}}\)