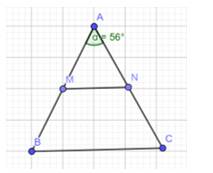
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)
a) Tính\(\widehat B\), \(\widehat C\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.
c) Chứng minh rằng MN // BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2022
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vì tam giác ABC cân tại A
\( \Rightarrow \widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ABF} = \widehat {ACE}\)
b) Xét \(\Delta ECA\) và \(\Delta FBA\)có:
\(\widehat{A}\) chung
AB = AC
\(\widehat {ABF} = \widehat {ACE}\)
\( \Rightarrow \)\(\Delta ECA\)= \(\Delta FBA\)( g – c – g )
\( \Rightarrow AE = AF và EC = BF\) (2 cạnh tương ứng)
\( \Rightarrow \Delta AEF\) cân tại A
c) Xét tam giác IBC có :
\(\widehat B = \widehat C \Rightarrow \dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat C \Rightarrow \widehat {ICB} = \widehat {IBC}\)
Do đó, tam giác IBC cân tại I ( 2 góc ở đáy bằng nhau )
\( \Rightarrow IB = IC\)( cạnh tương ứng )
Vì EC = BF ( câu b) và IB = IC
\( \Rightarrow \) EC – IC = BF – BI
\( \Rightarrow \) EI = FI
\( \Rightarrow \Delta IEF\) cân tại I
16 tháng 1 2020
a) +) Chứng minh \(\Delta\)DAC = \(\Delta\)BAE
Thật vậy: Ta có: AD = AB ( \(\Delta\)DAB đều )
^DAB = ^CAE ( = 60\(^o\); \(\Delta\)DAB đều ; \(\Delta\)CAE đều ) => ^DAC = ^BAE
CA = AE ( \(\Delta\)CAE đều )
Từ 3 điều trên => \(\Delta\)DAC = \(\Delta\)BAE ( c.g.c) (1)
=> ^ABE = ^ADC (2)
+) Xét \(\Delta\)KAD và \(\Delta\)KIB có: ^DKA = ^BKI ( đối đỉnh )
^KDA = ^KBI( theo ( 2) )
mà ^DKA + ^KDA + ^KAD= ^BKI + ^KBI + ^KIB = 180\(^o\)
=> ^KIB = ^KAD = ^BAD= 60\(^o\)
=> ^DIB = 60\(^o\)
b) Từ (1) => DC = BE mà M là trung điểm DC; N là trung điểm BE
=> DM = BN (3)
+) Xét \(\Delta\)BAN và \(\Delta\)DAM
có: BN = DM ( theo (3)
^ABN = ^ADM ( theo (2)
AB = AD ( \(\Delta\)ADB đều )
=> \(\Delta\)BAN = \(\Delta\)DAM (4)
=> AN = AM => \(\Delta\)AMN cân tại A (5)
+) Từ (4) => ^BAN = ^DAM => ^BAM + ^MAN = ^DAB + ^BAM
=> ^MAN = ^DAB = 60\(^o\)(6)
Từ (5); (6) => \(\Delta\)AMN đều
c) +) Trên tia đối tia MI lấy điểm F sao cho FI = IB => \(\Delta\)FIB cân tại I
mà ^BIF = ^BID = 60\(^{\text{}o}\)( theo (a))
=> \(\Delta\)FIB đều (7)
=> ^DBA = ^FBI( =60\(^o\))
=> ^DBF + ^FBA = ^FBA + ^ABI
=> ^DBF = ^ABI
Lại có: BI = BF ( theo (7) ) và BA = BD ( \(\Delta\)BAD đều )
Từ (3) điều trên => \(\Delta\)DFB = \(\Delta\)AIB => ^AIB = ^DFB = 180\(\text{}^o\)- ^BFI = 180\(\text{}^o\)-60\(\text{}^o\)=120\(\text{}^o\)
+) Mặt khác ^BID = 60 \(\text{}^o\)( theo (a) )
=> ^DIE = 180\(\text{}^o\)- ^BID = 120 \(\text{}^o\)và ^DIA = ^AIB - ^BID = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^AIE = ^DIE - ^DIA = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^DIA = ^AIE ( = 60\(\text{}^o\))
=> IA là phân giác ^DIE.
13 tháng 10 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
b: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
29 tháng 9 2018
MN là đường trung bình của \(\Delta ABC\Rightarrow MN//AC\Rightarrow\widehat{MNH}=\widehat{C}\)
HM là đường trung tuyến ứng với cạnh huyền AB của \(\Delta AHB\Rightarrow HM=MB=\frac{1}{2}AB\)
\(\Rightarrow\Delta HMB\)cân tại M \(\Rightarrow\widehat{MHB}=\widehat{B}=2\widehat{C}\)
Ta có: \(\widehat{MHB}=\widehat{HMN}+\widehat{MNH}\Rightarrow2\widehat{C}=\widehat{HMN}+\widehat{C}\Rightarrow\widehat{HMN}=\widehat{C}\)
Vậy \(\widehat{HMN}=\widehat{MHN}\left(=\widehat{C}\right)\) nên tam giác HMN cân
1 tháng 8 2023
.Ta có :
AH⊥BC,HE⊥AB→\(\widehat{AEH}=\widehat{AHB}\)
=> \(\Delta AEH\approx\Delta AHB\)(g.g)
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>AH\(^2\)=AE.AB
Lam tuong tu ta dc AH\(^2\)=AF.AC
=> AE.AB=AF.AC
1 tháng 8 2023
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nen AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC