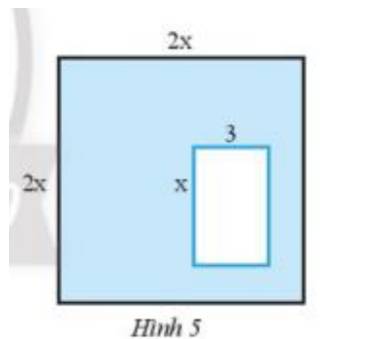
Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5). Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
Diện tích hình chữ nhật là \(2x.4x = 8{x^2}\)
Diện tích phần hình vuông là \({x^2}\)
Diện tích phần màu vàng còn lại là \(8{x^2} - {x^2} = 7{x^2}\)
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
Ta có diện tích hình chữ nhật lớn là : \((2x + 4)(3x + 2) = 2x(3x + 2) + 4(3x + 2) = 6{x^2} + 4x + 12x + 8 = 6{x^2} + 16x + 8\)
Diện tích hình chữ nhật nhỏ là : \(x(x + 1) = {x^2} + x\)
Diện tích phần cần tìm là : \(6{x^2} + 16x + 8 - {x^2} - x\)\( = 5{x^2} + 15x + 8\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h là \(60x\) (km).
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm là
\({(2x)^2} + 3.x + \dfrac{1}{2}.4.8 = 4{x^2} + 3x + 16\)
b) Các biểu thức trên có 1 biến (biến x). Mỗi số hạng xuất hiện trong biểu thức (60x, 4x2, 3x) đều là tích của một số nhân một biến và số hạng (8) là dạng số hoặc đơn thức với số mũ của x bằng 0.
H9
HT.Phong (9A5)
CTVHS
15 tháng 10 2023
a) Đa thức biểu thị chu vi hình chữ nhật là:
\(\left(2x+y+2x-y\right)\cdot2=4x\cdot2=8x\left(m\right)\)
b) Đa thức biểu thị diện tích hình chữ nhật là:
\(\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\)
c) Diện tích của mảnh vườn là:
\(4\cdot3^2-2^2=32\left(m^2\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
\(a,Chu.vi:2.\left(2x+y+2x-y\right)=2.4x=8x\left(m\right)\\ b,Diện.tích:\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\\ c,Thay:x=3;y=2.vào.biểu.thức.tính.diện.tích.thì.diện.tích.mảnh.vườn.là:\\ 4x^2-y^2=4.3^2-2^2=32\left(m^2\right)\)
dm2.
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
Diện tích phần màu xanh là
\(\dfrac{8}{5}\times\dfrac{8}{5}\times2=\dfrac{128}{25}\left(dm^2\right)\)
Đáp số: \(\dfrac{128}{25}\left(cm^2\right)\)
24 tháng 8 2023
Diện tích hình vuông nhỏ là (8/5)^2=64/25m2
Diện tích phần màu xanh là:
64/25*2=128/25m2
26 tháng 1
phép nhân đó được thực hiện bằng cách lấy từng hạng tử của đa thức M nhân với từng hạng tử của đa thức N rồi sau đó cộng tổng lại với nhau và ra kết quả
Kết quả chắc chắn sẽ là một đa thức
CM
7 tháng 3 2018
Điểm thuộc đồ thị có y = 6 thì ứng với x = 2 .
Vậy khi diện tích hình chữ nhật bằng 6(m2) thì cạnh x = 2 (m)
Điểm thuộc đồ thị có y = 9 thì ứng với x = 3.
Vậy khi diện tích hình chữ nhật bằng 9 (m2) thì cạnh x = 3 (m)
CM
22 tháng 2 2018
- Công thức biểu diễn diện tích y theo x là y = 3x
- Vì với mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số đại lượng x
- Vẽ đồ thị hàm số :
+ Chọn 1 điểm khác O thuộc đồ thị : chọn x = 1 được y = 3 ⇒ A(1 ;3) thuộc đồ thị.
+ Đường thằng OA là đồ thị hàm số y = 3x
Vẽ đồ thị:
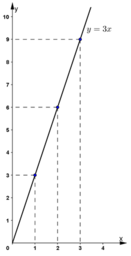
Trên đồ thị thấy :
+ Điềm thuộc đồ thị có x = 3 thì ứng với y = 9
Vậy khi x = 3 m thì diện tích hình chữ nhật bằng 9(m2)
+ Điểm thuộc đồ thị có x = 4 thì ứng với y = 12
Vậy khi x = 4 m thì diện tích hình chữ nhật bằng 12 (m2)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Cộng hai đa thức:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
- Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết tổng hai đơn thức theo hàng ngang;
- Nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
b) Trừ hai đa thức:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Diện tích hình vuông là : \(2x.2x = 4{x^2}\)
Diện tích hình chữ nhật là : \(3.x = 3x\)
Diện tích phần cần tìm là : \(4{x^2} - 3x\)