Cho △ ABC vuông tại A có AB=3cm Ac=4cm đường cao AH gọi E và F là hình chiếu của H trên AB và. Tính diện tích AEHF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
27 tháng 10 2023
Đúng(0)
Những câu hỏi liên quan
12 tháng 7 2023
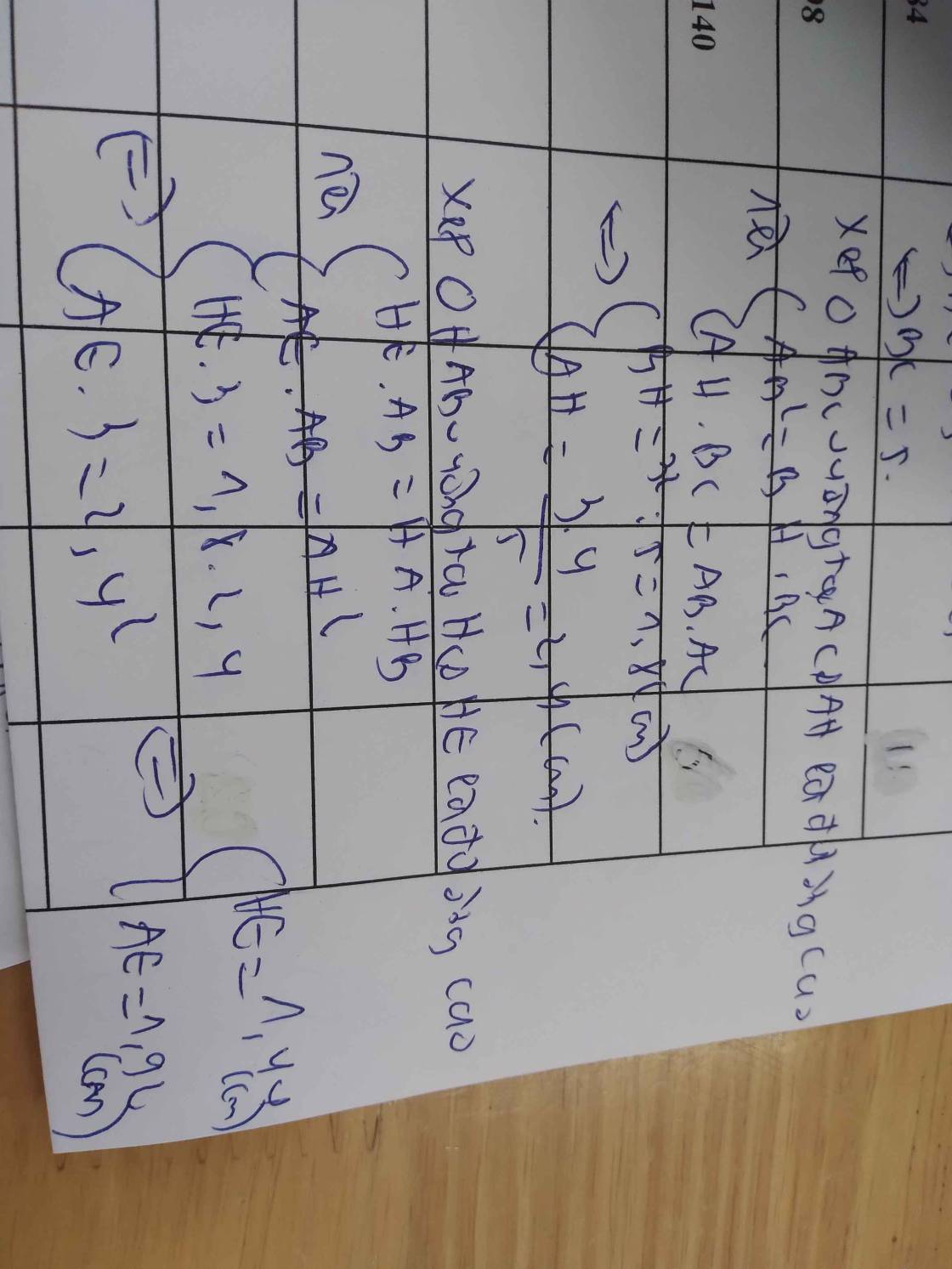
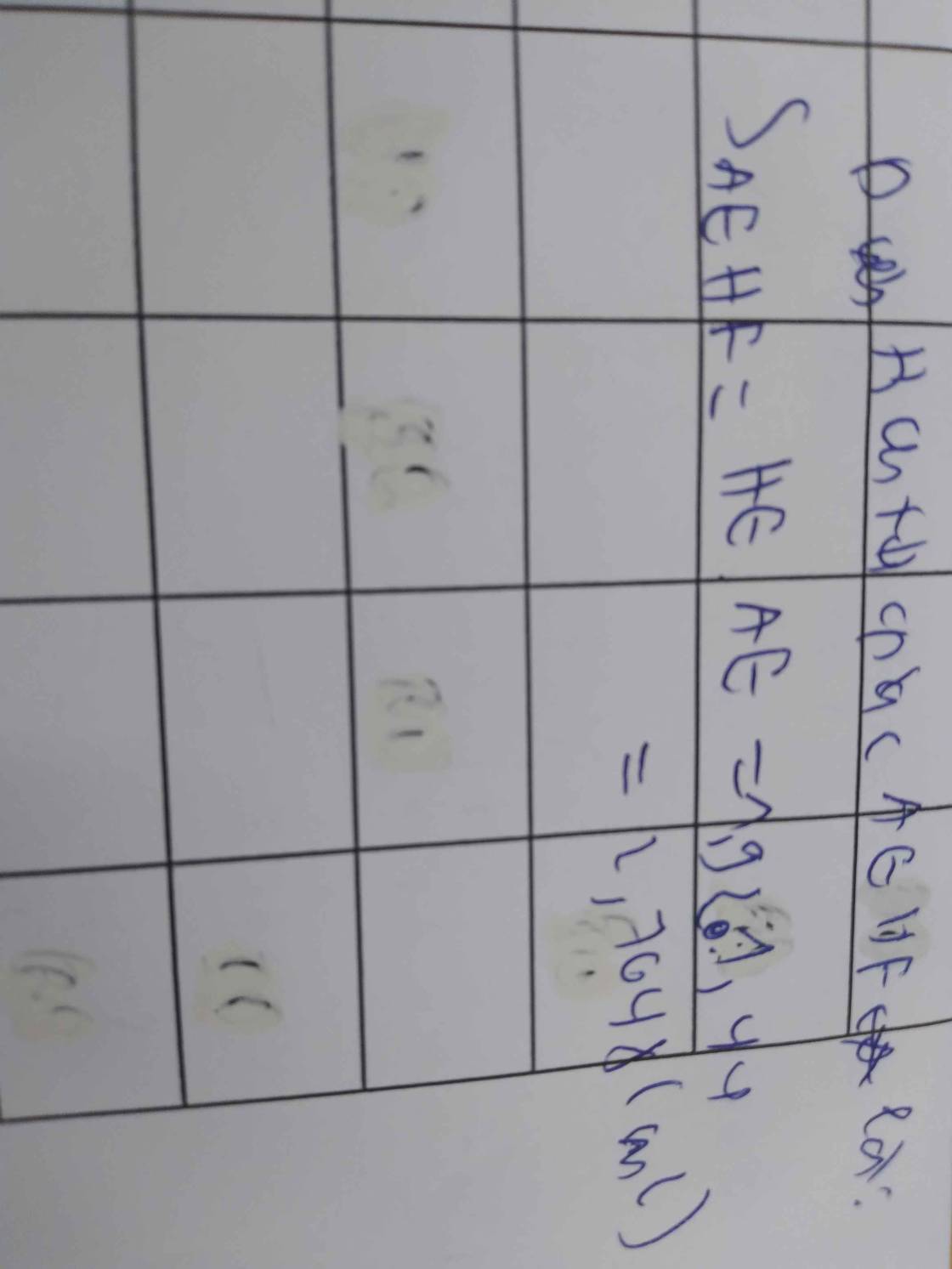
AC=căn 10^2-8^2=6cm
AH=6*8/10=4,8cm
AE=AH^2/AB=4,8^2/8=2,88cm
AF=AH^2/AC=4,8^2/6=3,84cm
S AEF=1/2*2,88*3,84=5,5296cm2
S ABC=1/2*6*8=24cm2
=>S BEFC=24-5,5296=18,4704cm2
2 tháng 11 2021
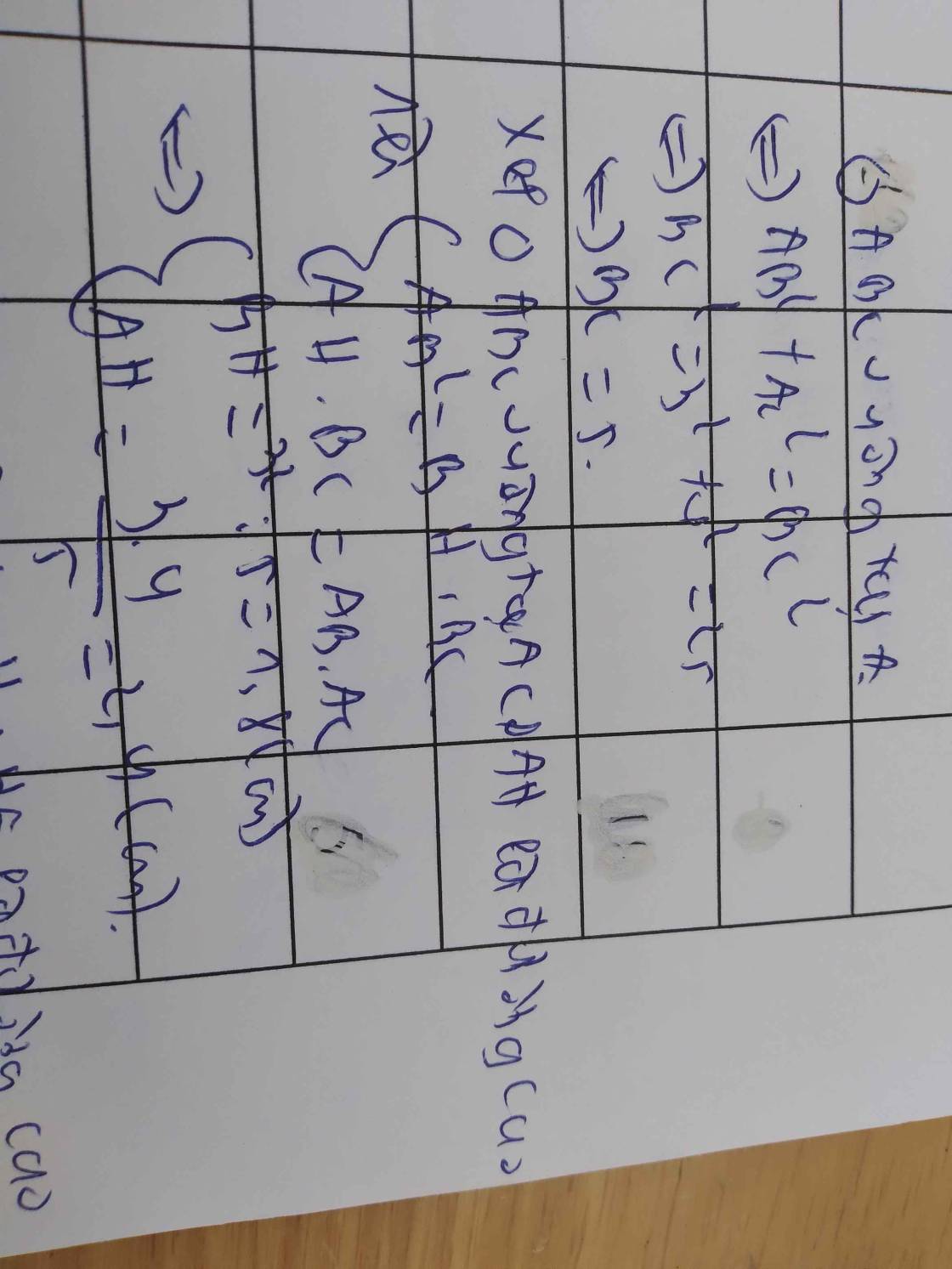
a: CH=6cm
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(\widehat{C}=30^0\)
23 tháng 10 2021
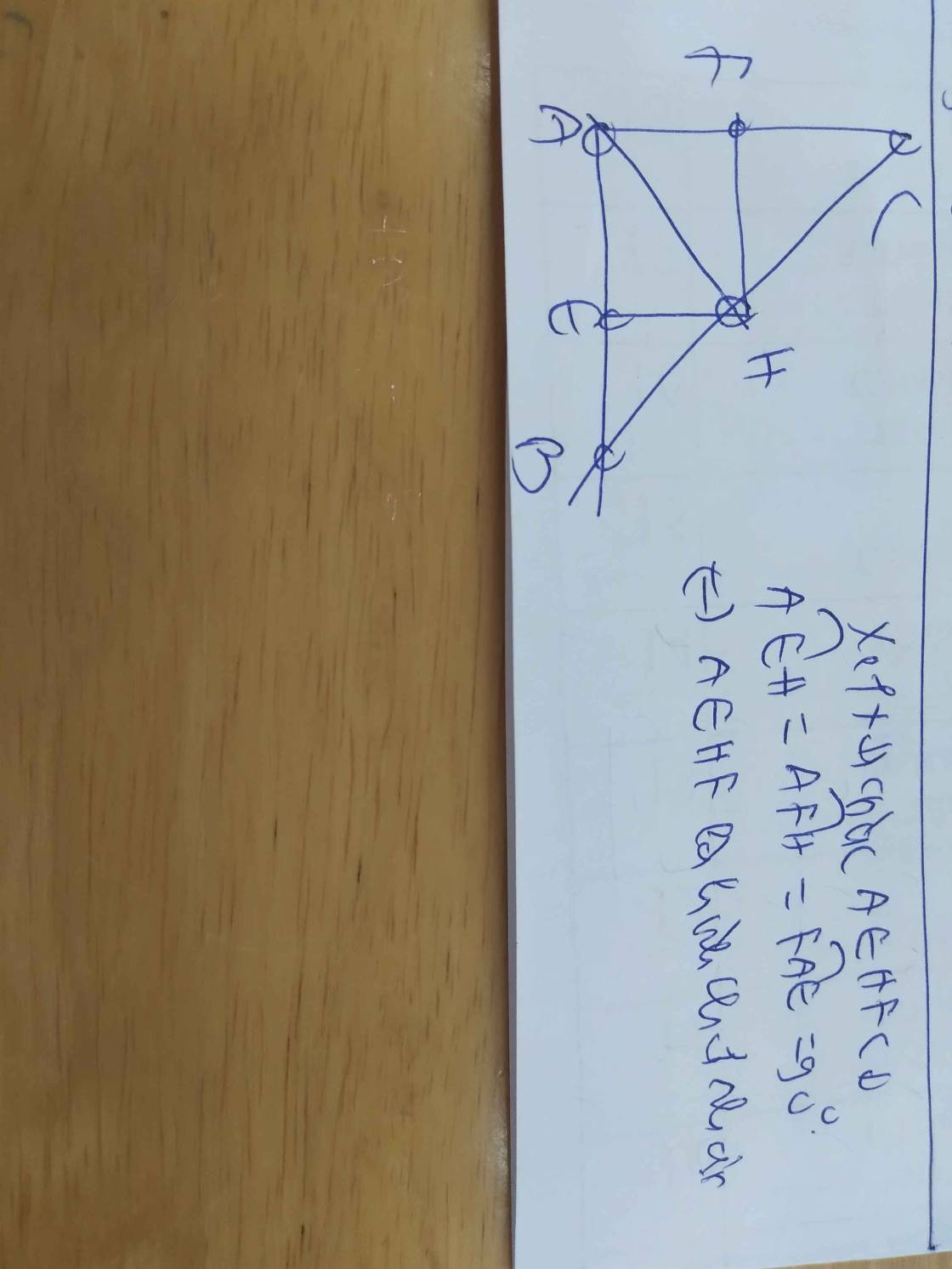
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
24 tháng 10 2021
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
CM
6 tháng 8 2019
Theo chứng minh trên, ta có:
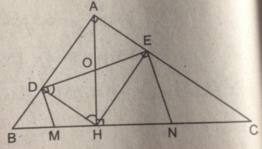
DM = MH = 1/2 BH = 1/2.4 = 2(cm)
EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)
DE = AH = 6(cm)
DENM là hình thang vuông, do đó diện tích của nó là:
S D E N M = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5( c m 2 ).