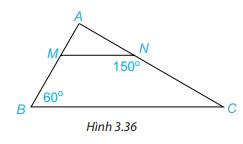
1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \).
Hãy tính số đo các góc BMN và ACB.
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không?

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó, \(\widehat{ADC}=90^0\)
Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Vậy \(\widehat{ADC}=90^0; \widehat {ABC} = 50^\circ \)

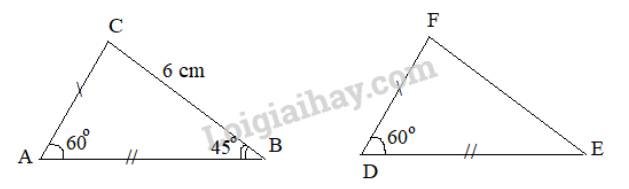
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)

Do \(\Delta ABC = \Delta DEF\) nên \(\widehat B = \widehat E = {80^o}\); \(\widehat D = \widehat A = {60^o}\); \(\widehat C = \widehat F\) ( các góc tương ứng)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 60^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 60^\circ - 80^\circ = 40^\circ \end{array}\)
Do đó \(\widehat F = 40^\circ \)
Vậy \(\widehat B = {80^o}; \widehat D ={60^o}; \widehat C = \widehat F= 40^\circ \).

Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)


Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).

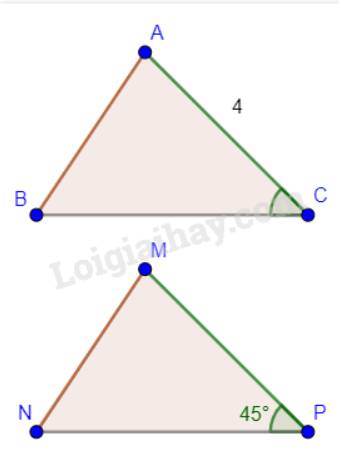
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).

Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)
1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \)
Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\)
Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \).
2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong)
Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \)
Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.