Tính:
\(\begin{array}{l}a){\left( { - \frac{4}{5}} \right)^4}\\b){(0,7)^3}\end{array}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
\(\begin{array}{l}a)x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\\x = \dfrac{9}{{20}} + \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right)\\x = \dfrac{9}{{20}} + \dfrac{{25}}{{20}} - \dfrac{{28}}{{20}}\\x = \dfrac{{6}}{{20}}\\x = \dfrac{{ 3}}{{10}}\end{array}\)
Vậy \(x = \dfrac{{ 3}}{{10}}\)
\(\begin{array}{*{20}{l}}{b)9 - x = \dfrac{8}{7} - \left( { - \dfrac{7}{8}} \right)}\\\begin{array}{l}9 - x = \dfrac{8}{7} + \dfrac{7}{8}\\9 - x = \dfrac{{64}}{{56}} + \dfrac{{49}}{{56}}\\9 - x = \dfrac{{113}}{{56}}\end{array}\\{x = 9 - \dfrac{{113}}{{56}}}\\{x = \dfrac{{504}}{{56}} - \dfrac{{113}}{{56}}}\\{x = \dfrac{{391}}{{56}}}\end{array}\)
Vậy \(x = \dfrac{{391}}{{56}}\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
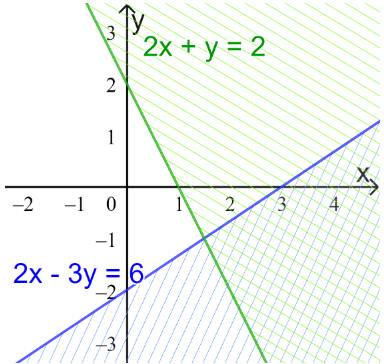
a) Vẽ các đường thẳng \(2x - 3y = 6;2x + y = 2\) (nét đứt)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 2.0-3.0
=> O thuộc miền nghiệm của cả 2 bất phương trình
Miền nghiệm:
b)
Vẽ các đường thẳng
\(4x + 10y \le 20 \Leftrightarrow y = - \frac{2}{5}x + 2\) (nét liền)
\(x - y = 4 \Leftrightarrow y = x - 4\)(nét liền)
\(x = - 2\)(nét liền)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 4.0+10.0-2
=> O thuộc miền nghiệm của cả 3 bất phương trình
Miền nghiệm:
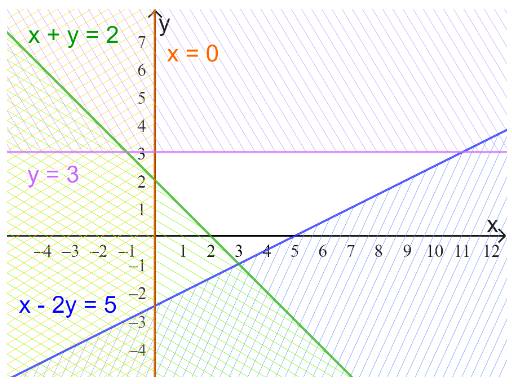
c)
Vẽ các đường thẳng
\(x - 2y = 5 \Leftrightarrow y = \frac{1}{2}x - 5\) (nét liền)
\(x + y = 2 \Leftrightarrow y = - x + 2\)(nét liền)
\(y = 3\)(nét liền)
Và trục Oy
Thay tọa độ O vào bất phương trình \(x - 2y \le 5\)
=> O thuộc miền nghiệm của bất phương trình trên.
Thay tọa độ O vào \(x + y \ge 2\)
=> O không thuộc miền nghiệm của bất phương trình trên
Lấy phần bên phải trục Oy và bên dưới đường thẳng y=3
Miền nghiệm:
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Vẽ các đường thẳng \(x + 2y = - 4\)(nét đứt) và \(y = x + 5\) (nét liền)
Thay tọa độ O vào \(x + 2y < - 4\) ta được: \(0 + 2.0 < - 4\) (Sai)
=> Gạch đi phần chứa O.
Thay tọa độ O vào \(y \ge x + 5\) ta được: \(0 \ge 0 + 5\) (Sai)
=> Gạch đi phần chứa O.
\(x + 2y = -4 => y = \frac{-4 - x}{2} \)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(x + 2y = - 4\) và \(y = x + 5\), ta được:
\( \frac{-4 - x}{2} = x + 5 \\ x = \frac{-14}{3} \\ => y = \frac{1}{3} \)
Miền nghiệm của hệ:
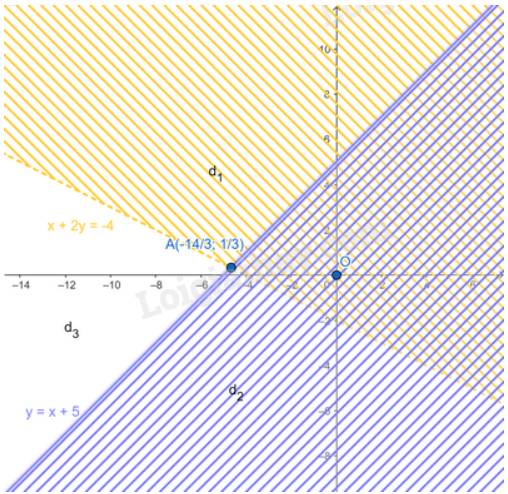
Từ hình vẽ ta thấy miền nghiệm của hệ là \(d_3\)
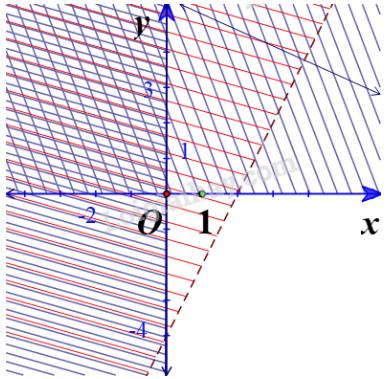
b) Vẽ các đường thẳng \(4x - 2y = 8\)(nét đứt) và hai trục (nét liền)
Thay tọa độ O vào \(4x - 2y > 8\) ta được: \(4.0 - 2.0 > 8\) (Sai)
=> Gạch đi phần chứa O.
Với \(x \ge 0\) thì gạch phần bên trái Oy
Với \(y \le 0\) thì gạch bên trên Ox
Miền nghiệm của hệ:
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
\(\begin{array}{l}a)\frac{{{3^{12}} + {3^{15}}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}} + {3^{12}}{{.3}^3}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}}.(1 + {3^3})}}{{1 + {3^3}}}\\ = {3^{12}}\\b)2:{\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 0,{125^3}{.8^3} - {( - 12)^4}:{6^4}\\ = 2:{\left( {\frac{3}{6} - \frac{4}{6}} \right)^2} + {(0,125.8)^3} - {12^4}:{6^4}\\ = 2:{\left( {\frac{{ - 1}}{6}} \right)^2} + {1^3} - {(\frac{{12}}{6})^4}\\ = 2:\frac{1}{{36}} + 1 - {2^4}\\ = 2.36 + 1 - 16\\ = 72 + 1 - 16=57\end{array}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a, Điều kiện xác định: \(\frac{1}{2}x + \frac{\pi }{4} \ne k\pi \Leftrightarrow x \ne - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)
Ta có: \(cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = - 1 \Leftrightarrow cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = \cot \left( { - \frac{\pi }{4}} \right)\)
\( \Leftrightarrow \frac{1}{2}x + \frac{\pi }{4} = - \frac{\pi }{4} + k\pi \Leftrightarrow x = - \pi + k2\pi ,k \in \mathbb{Z}\,\,(TM).\)
Vậy \(x = - \pi + k2\pi ,k \in \mathbb{Z}\,\).
b, Điều kiện xác định: \(3x \ne k\pi \Leftrightarrow x \ne k\frac{\pi }{3},k \in \mathbb{Z}.\)
\(\;cot3x = - \frac{{\sqrt 3 }}{3} \Leftrightarrow cot3x = \cot \left( { - \frac{\pi }{3}} \right)\)
\( \Leftrightarrow 3x = - \frac{\pi }{3} + k\pi \Leftrightarrow x = - \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\,(TM).\)
Vậy \(x = - \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
\(\begin{array}{l}a){\left( {\frac{2}{3}} \right)^{10}}{.3^{10}} = \frac{{{2^{10}}}}{{{3^{10}}}}{.3^{10}} = {2^{10}}\\b){( - 125)^3}:{25^3} = {( - 125:25)^3} = {( - 5)^3} = - 125\\c){(0,08)^3}{.10^6} = {(0,08)^3}{.100^3} = {(0,08.100)^3} = {8^3}\end{array}\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
\(\begin{array}{l}a)A = 32,125 - (6,325 + 12,125) - (37 + 13,675)\\ = 32,125 - 6,325 - 12,125 - 37 - 13,675\\ = (32,125 - 12,125) + ( - 6,325 - 13,675) - 37\\ = 20 + ( - 20) - 37\\ = - 37\\b)B = 4,75 + {\left( {\frac{{ - 1}}{2}} \right)^3} + 0,{5^2} - 3.\frac{{ - 3}}{8}\\ = 4,75 + \frac{{ - 1}}{8} + 0,25 + \frac{9}{8}\\ = (4,75 + 0,25) + \left( {\frac{{ - 1}}{8} + \frac{9}{8}} \right)\\ = 5 + \frac{8}{8}\\ = 5 + 1\\ = 6\\c)C = 2021,2345.2020,1234 + 2021,2345.( - 2020,1234)\\ = 2021,2345.[2020,1234 + ( - 2020,1234)]\\ = 2021,2345.0\\ = 0\end{array}\)
DT
27 tháng 4 2022
\(\left\{{}\begin{matrix}\dfrac{3}{x-1}+\dfrac{4}{y}=13\\\dfrac{2}{x-1}-\dfrac{5}{y}=1\end{matrix}\right.\)(1)
ĐK: \(\left\{{}\begin{matrix}x-1\ne0\\y\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\y\ne0\end{matrix}\right.\)
Đặt \(u=\dfrac{1}{x-1};v=\dfrac{1}{y}\)
\(\left(1\right)\Rightarrow\left\{{}\begin{matrix}3u+4v=13\\2u-5v=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6u+8v=26\\6u-15v=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}23v=23\\2u-5v=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v=1\\2u=1-5v=1+5.1=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v=1\\u=\dfrac{6}{2}=3\end{matrix}\right.\)
- Khi u= 3, ta có \(\dfrac{1}{x-1}=3\Leftrightarrow1=3\left(x-1\right)\Leftrightarrow1=3x-3\)
\(\Leftrightarrow3x=4\Leftrightarrow x=\dfrac{4}{3}\)(thỏa mãn)
- Khi v= 1, ta có: \(\dfrac{1}{y}=1\Leftrightarrow y=1\)(thỏa mãn)
Vậy nghiệm của hệ phương trình là: \(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=1\end{matrix}\right.\)
\(\begin{array}{l}a){\left( { - \frac{4}{5}} \right)^4} = \left( { - \frac{4}{5}} \right).\left( { - \frac{4}{5}} \right).\left( { - \frac{4}{5}} \right).\left( { - \frac{4}{5}} \right)\\ = \frac{{16}}{{25}}.\frac{{16}}{{25}}\\ = \frac{{256}}{{625}}\\b){(0,7)^3} = 0,7.0,7.0,7\\ = 0,49.0,7\\ = 0,343\end{array}\)