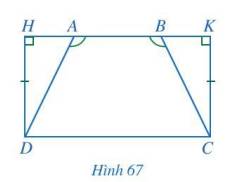
Cho Hình 67 có \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,DH = CK,\widehat {DAB} = \widehat {CBA}\). Chứng minh AD = BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.
Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền - cạnh góc vuông)
Nên AD = BC ( 2 cạnh tương ứng)

Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)

a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)

Ta có: tổng ba góc trong một tam giác bằng 180° và \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\) nên \(\widehat {PQM} = \widehat {NMQ}\).
Xét hai tam giác MNQ và QPM có:
\(\widehat {NQM}=\widehat {PMQ}\)
MQ chung
\(\widehat {NMQ}=\widehat {PQM}\)
Vậy \(\Delta MNQ = \Delta QPM\)(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)


\(\Delta SAB,\Delta SAC\) đều \( \Rightarrow AB = {\rm{A}}C = a\)
\(BC = \sqrt {S{B^2} + S{C^2}} = a\sqrt 2 \)
\( \Rightarrow \Delta ABC\) vuông cân tại \(A\)
\(AJ\) là trung tuyến của tam giác \(ABC\)\( \Rightarrow AJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBC\) vuông cân tại \(S\) có \(SJ\) là trung tuyến
\( \Rightarrow SJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(IJ\) là trung tuyến của tam giác \(SAJ\)\( \Rightarrow IJ = \frac{{\sqrt {2\left( {A{J^2} + S{J^2}} \right) - S{A^2}} }}{2} = \frac{a}{2}\)
\(AI = \frac{1}{2}SA = \frac{a}{2};BJ = \frac{1}{2}BC = \frac{a}{2}\)
Xét tam giác \(AIJ\) có: \(A{I^2} + I{J^2} = A{J^2}\)
\( \Rightarrow \Delta AIJ\) vuông tại \(I\)\( \Rightarrow AI \bot IJ \Rightarrow SA \bot IJ\)
\(\Delta SAB\) đều \( \Rightarrow BI = \sqrt {A{B^2} - A{I^2}} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(BIJ\) có: \(B{J^2} + I{J^2} = B{I^2}\)
\( \Rightarrow \Delta BIJ\) vuông tại \(J\)\( \Rightarrow BJ \bot IJ \Rightarrow BC \bot IJ\)

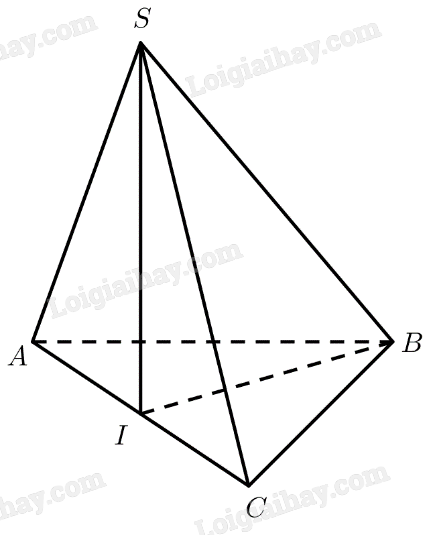
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)

a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân

a, \(\Delta HCI=\Delta DCI\left(ch-gn\right)\Rightarrow HI=DI=AI=\frac{1}{2}AD\)
\(\Delta AHD\)có đường trung tuyến \(HI=\frac{1}{2}AD\)
\(\Rightarrow\Delta AHD\)vuông tại H \(\Rightarrow\widehat{AHD}=90^0\)
b, \(\Delta AIB=\Delta HIB\left(ch-cgv\right)\Rightarrow\widehat{ABI}=\widehat{HBI}\)
Do đó: BI là tia p/g của \(\widehat{ABC}\)
Mà CI là tia phân giác của \(\widehat{BCD}\)
\(\widehat{ABC}+\widehat{BCD}=180^0\)
\(\Rightarrow\widehat{BIC}=90^0\)
c, \(\Delta HCI=\Delta DCI\left(cmt\right)\Rightarrow HC=DC\)(1)
\(\Delta ABI=\Delta HBI\left(cmt\right)\Rightarrow AB=HB\) (2)
Từ (1) và (2), ta được \(AB+DC=HB+HC=BC\)
Ta có: \(\widehat {DAB} = \widehat {CBA}\)
Mà \(\widehat {DAB} +\widehat {HAD} =180^0; \widehat {CBA}= \widehat {KBC}\) (2 góc kề bù)
\(\Rightarrow \widehat {HAD} = \widehat {KBC}\)
Mà tổng ba góc trong tam giác bằng 180° và \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,\widehat {HAD} = \widehat {KBC}\) nên \(\widehat {ADH} = \widehat {BCK}\).
Xét tam giác AHD và tam giác BKC có:
\(\widehat {AHD} = \widehat {BKC}\);
HD = KC;
\(\widehat {ADH} = \widehat {BCK}\).
Vậy \(\Delta AHD = \Delta BKC\)(g.c.g) nên AD = BC ( 2 cạnh tương ứng)