Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
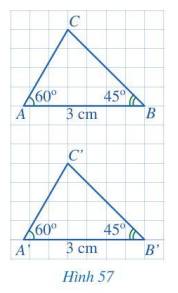


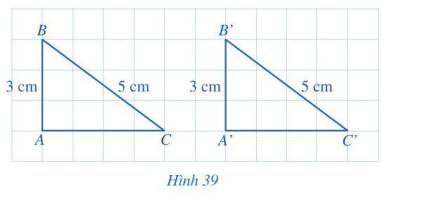
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)