Trong các khẳng định sau, khẳng định nào đúng?
A. Hai tam giác đồng dạng thì bằng nhau.
B. Hai tam giác bằng nhau thì đồng dạng.
C. Hai tam giác bằng nhau thì không đồng dạng.
D. Hai tam giác cân thì luôn đồng dạng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khẳng định đúng là a, khẳng định sai là b.
- Khẳng định a đúng vì
Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
- Khẳng định b sai vì
Nếu\(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) thì tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi \(k \ne 1\) thì \(AB \ne A'B';AC \ne A'C';BC \ne B'C'\) nên hai tam giác không bằng nhau.

a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)

a) Mệnh đề Đúng.
Giả sử có ΔABC = ΔA’B’C’
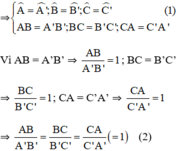
Từ (1) và (2) suy ra 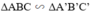
b) Mệnh đề Sai.
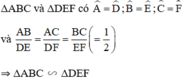
nhưng ΔABC và ΔDEF không bằng nhau
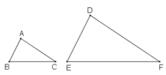

Khẳng định sai là :
C.nếu AB=DE và B=E thì hai tam giác trên bằng nhau
# học tốt #

a: Đúng
Vì ΔABC=ΔDEF
nên AB=DE; BC=EF; AC=DF
=>CABC=CDEF
c: Đúng vì ΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^0\)
d: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow3\cdot\widehat{B}=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{B}=40^0\)
=>\(\widehat{A}=80^0\)(đúng)
Đáp án đúng là B
Hai tam giác bằng nhau thì đồng dạng với tỉ số đồng dạng \(k = 1\).