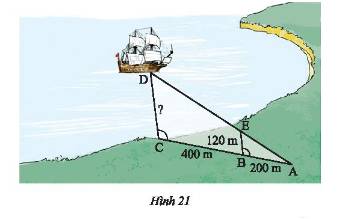
Với số liệu được ghi trên Hình 21. Hãy tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
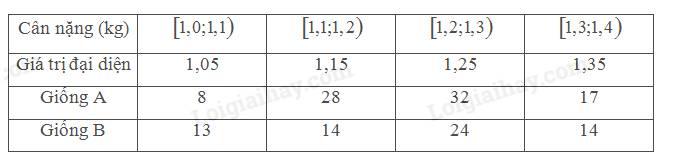
Số trung bình của số liệu là: \(\bar x \approx 192,41\)
Tứ phân vị thứ nhất là: \({x_5} = 165,6\)
Tứ phân vị thứ hai là: \({x_{10}} = 173\)
Tứ phân vị thứ ba là: \({x_{15}} = 220,7\)
Giá trị xuất hiện nhiều nhất là \({M_O} = 165,9\)
b)
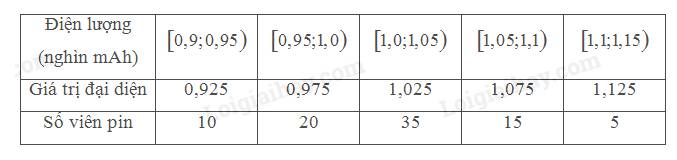
c) Ta có:
• Lượng mưa trung bình trong tháng 8 là:
\(\bar x = \frac{{10.147,5 + 5.202,5 + 3.257,5 + 1.312,5}}{{19}} \approx 188,03\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\).
Do đó: \({u_m} = 120;{n_{m - 1}} = 0;{n_m} = 10;{n_{m + 1}} = 5;{u_{m + 1}} - {u_m} = 175 - 120 = 55\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{120 - 0}}{{\left( {120 - 0} \right) + \left( {120 - 5} \right)}}.55 \approx 148,09\)
• Gọi \({x_1};{x_2};...;{x_{19}}\) là lượng mưa trong tháng 8 được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}}\end{array};{x_{11}},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {175;230} \right)}\end{array};{x_{16}},{x_{17}},{x_{18}} \in \begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array};{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {285;340} \right)}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{10}}\)
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_{10}} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{2} - 0}}{{10}}.\left( {175 - 120} \right) = 172,25\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_5}\).
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_5} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{4} - 0}}{{10}}.\left( {175 - 120} \right) = 146,125\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{16}}\).
Ta có: \(n = 19;{n_j} = 3;C = 10 + 5 = 15;{u_j} = 230;{u_{j + 1}} = 285\)
Do \({x_{16}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 230 + \frac{{\frac{{3.19}}{4} - 15}}{3}.\left( {285 - 230} \right) = 216,25\)
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(\widehat {ABE} = \widehat {ACD} \Rightarrow BE//CD\) (hai góc đồng vị bằng nhau)
Trong tam giác \(ACD\) có \(BE//CD\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}}\) mà \(AC = AB + BC = 8 + 8 = 16\)
Suy ra, \(\frac{8}{{16}} = \frac{3}{{CD}} \Rightarrow CD = \frac{{3.16}}{8} = 6\).
Vậy bề rộng \(CD\) của con sông là 6m.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
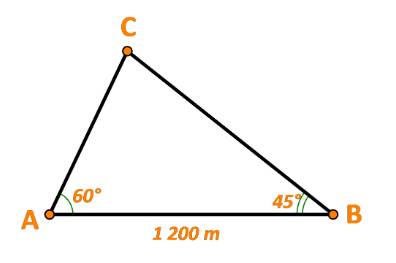
Ta có: \(\widehat C = {180^o} - {60^o} - {45^o} = {75^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \frac{{\sin B.AB}}{{\sin C}}\\BC = \frac{{\sin A.AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \frac{{\sin {{45}^o}.1200}}{{\sin {{75}^o}}} \approx 878\\BC = \frac{{\sin {{60}^o}.1200}}{{\sin {{75}^o}}} \approx 1076\end{array} \right.\)
Vậy AC = 878 m, BC = 1076 m.
VT
31 tháng 10 2019
a) Chọn S1 đối xứng S qua gương M1 ; Chọn O1 đối xứng O qua gương M2 , nối S1O1 cắt gương M1 tại I , gương M2 tại J. Nối SIJO ta được tia cần vẽ
b) DS1AI ~ D S1BJ
Þ A I B J = S 1 A S 1 B = a a + d
Þ AI = a a + d .BJ (1)
Xét DS1AI ~ D S1HO1
Þ A I H O 1 = S 1 A S 1 H = a 2 d
Þ AI = a 2 d . h thay vào (1) ta được BJ = ( a + d ) . h 2 d
10 tháng 3 2022
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=20cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1}{h'}=\dfrac{30}{20}\Rightarrow h'=\dfrac{2}{3}cm\)
22 tháng 9 2023
Tham khảo:
a) Số xe trung bình đi qua trạm thu phí trong mỗi phút là: \(\bar x \approx 17,4\) (xe).
b)
c) Do số xe là số nguyên nên ta hiệu chỉnh lại như sau:
Số xe trung bình đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm là:
\(\bar x = \frac{{5.8 + 9.13 + 3.18 + 9.23 + 4.28}}{{30}} \approx 17,7\)
Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).