Tìm độ dài \(x\) trên Hình 13.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 10 2019
- Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
- Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
⇒ x = √5
- Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 - 212 = 841 - 441 = 400
⇒ x = 20
- Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16
⇒ x = 4
tìm độ dài x trên các hình 124,125
18 tháng 1 2021
Hình 124Theo định lí Pi-ta-go ta có:AC^2-BC^2=AB^2⇒10^2-8^2=AB^2⇒100-64=AB^2⇒36=AB^2⇒AB=6 (Vì AB>0)Hình 125Theo định lí Pi-ta-go ta có:DE^2+DF^2=EF^2⇒1^2+1^2=EF^2⇒1+1=EF^2⇒2=EF^2⇒EF=2 (vì EF>0)
CM
15 tháng 6 2017
Áp dụng định lí Py – ta – go
Tam giác ABC vuông tại B
⇒ x2 + 82 = 102
⇒ x2 = 102 – 82 = 36
⇒ x = 6 (cm)
Tam giác DEF vuông tại D
⇒ 12 + 12 = x2
⇒ x2 = 1 + 1 = 2
⇒ x = √2 (cm)
QT
2
13 tháng 9 2023
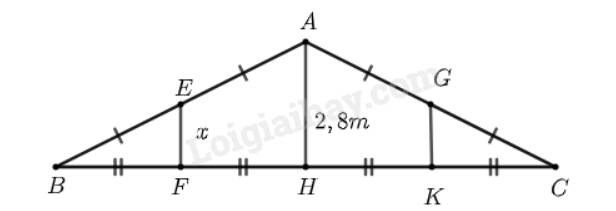
Theo hình vẽ ta có:
\(BE = EA \Rightarrow E\) là trung điểm của \(AB\);
\(BF = FH \Rightarrow F\) là trung điểm của \(BH\).
Vì \(E\)là trung điểm của \(AB\); \(F\)là trung điểm của \(BH\) nên \(EF\) là đường trung bình của tam giác \(ABH\).
\( \Rightarrow EF = \frac{1}{2}AH\) (tính chất đường trung bình)
\( \Leftrightarrow EF = \frac{1}{2}.2,8 = 1,4\).
Vậy \(x = 1,4m\).
N
2
BF
11 tháng 3 2023
A B C D
Áp dụng định lý Pitago vào `ΔABD`
`=> AD^2 + AB^2 = BC^2`
`=> AD^2 = BC^2 - AB^2 `
`=> AD^2 = 13^2 - 12^2 `
`=> AD^2 = 25`
`=> AD = 5 (`Vì `AD > 0)`
`S_(ABCD) = 5 xx 12 = 60`
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
Áp dụng định lý Pitago trong tam giác vuông ABD:
\(AD=\sqrt{BD^2-AB^2}=\sqrt{13^2-12^2}=5\)
\(S_{ABCD}=AB.AD=60\)
5 tháng 3 2018
Tổng độ dài hai đáy là :
455 x 2 : 13 = 70 [ m ]
Đáy lớn là :
[ 70 + 15 ] : 2 = 42,5 [ m ]
Đáy bé là :
70 - 42,5 = 27,5 [ m ]
Đ/s : . . .
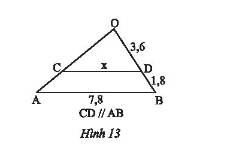
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).