cho tam giác abc có a^2 +b^2 -c^2 > 0 khi đó góc c sẽ ntn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn

Đáp án C
![]()
![]()
Suy ra phương trình mặt phẳng (ABC) là x+ y + z +1=0
Diện tích tam giác ABC là
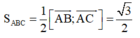
Góc giữa hai mặt phẳng (ABC) và α là
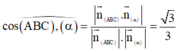
Khi đó diện tích tam giác A'B'C' là S A ' B ' C ' = S A B C . cos ( A B C ; α ) ^ = 1 2
Chú ý lý thuyết: Nếu đa giác (H) trong mặt phẳng (P) có diện tích S, đa giác (H) trong mặt phẳng là hình chiếu vuông góc (H) của có diện tích S', φ là góc giữa (P), (P') thì S ' = S . cos φ

Gọi CF là phân giác của góc C=> gACF=gBCF.
Ta lại có gBAC=1/2 gACB => g.BAC =g.ACF (=1/2g.ACB)=> Tam giác AFC cân tại F.
Vẽ FE vuông góc với AC(E thuộc AC). Tam giác AFC cân tại F => EA=EC=1/2AC mà AC=2BC => EC=BC.
Xét tam giác BCF và tam giác ECF, ta có:
EC=BC
g.ECF =g.BCF(CF là phân giác của g.ACB)
FC chung
Do đó: tgBCF =tgECF(c.g.c) => g.ABC=g.CEF=90o
Vậy tam giác ABC vuông tại B.
a^2+b^2-c^2>0
=>a^2+b^2>c^2
=>a^2+b^2>a^2+b^2-2ab*cosC
=>2ab*cosC>0
=>cosC>0
=>góc C<90 độ