Giúp em bài này với ạ: Cho hình thang ABCD có 2 đường chéo vuông góc với nhau, AB//CD. Biết AC= 16cm, BD=12cm. Tính đường cao. PLEASEEEE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
AN
0


DD
Đoàn Đức Hà
Giáo viên
22 tháng 6 2021
Dựng hình bình hành \(ABEC\).
Khi đó \(E\in DC\).
Vì \(BD\perp AC\)mà \(AC//BE\)nên \(BE\perp BD\).
Kẻ \(BH\perp DE\).
Xét tam giác \(BED\)vuông tại \(B\)đường cao \(BH\):
\(\frac{1}{BH^2}=\frac{1}{BD^2}+\frac{1}{BE^2}\Leftrightarrow\frac{1}{4^2}=\frac{1}{5^2}+\frac{1}{BE^2}\Leftrightarrow BE=\frac{20}{3}\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.BD.BE=\frac{1}{2}.5.\frac{20}{3}=\frac{50}{3}\left(cm^2\right)\)

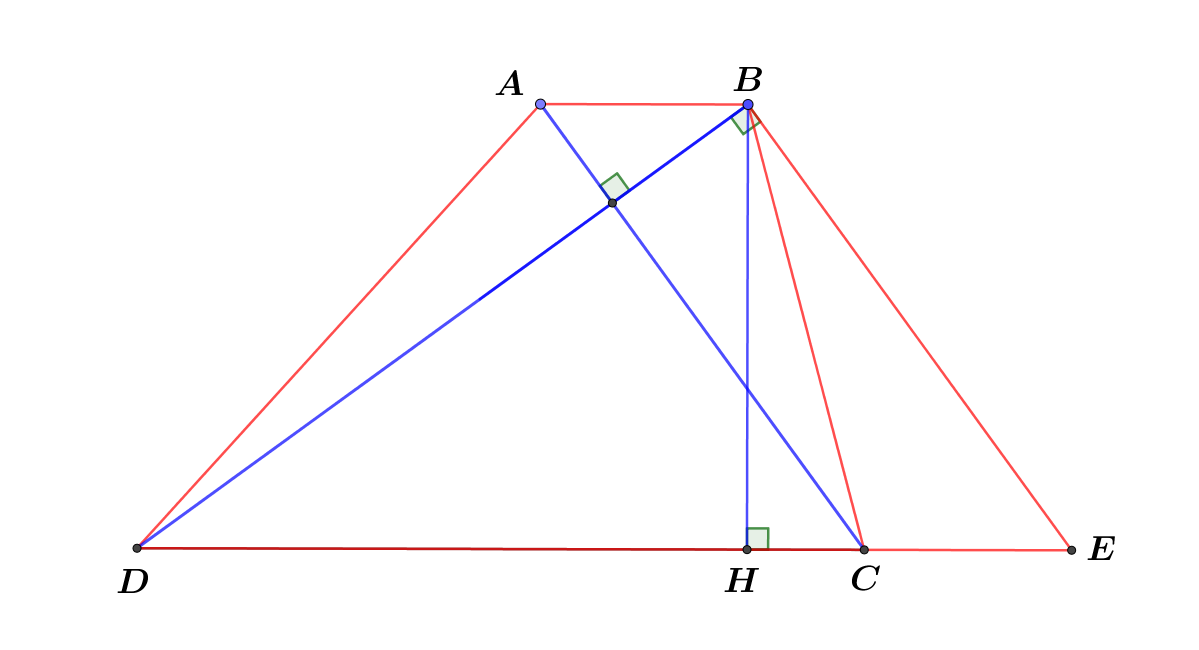
cách 1
Giả sử AB<CD; từ B kẻ đường thẳng//AC, cắt DC kéo dài tại E --> ABEC là hình bình hành vì có các cạnh đối // từng đôi một. Vì AC vuông góc với BD nên EB vuông góc với BD --> DE^2=BD^2+BE^2 =12^2 +16^2 =20^2 --> DE=20 cm. Mà DE=CD+CE và CE=AB ---> AB+CD=20cm
S(ABCD)= AC.BD/2=12.16/2= 96cm2
S(ABCD)= (AB+CD).h/2 =20h/2 =10h
10.h= 96 --> h= 9,6 cm
cách 2
Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Gọi BH là đường cao của hình thang.
Ta có ABEC là hình bình hành (cặp cạnh tương ứng song song) =>BE = AC = 16cm
mà AC vuông góc với BD (gt) => BE vuông góc với BD
CÁCH 1 :
Áp dụng pytago vào tam giác vuông BDE =>DE = 20 cm ( tam giác 3:4:5 ).
Mặt khác ta có : BH.DE = BD.BE ( cùng = 2 lần diện tích tam giác BDE hay có thể sử dụng tam giác đồng dạng để suy ra điều này) => BH = 12.16/20 = 9,6 (cm)
CÁCH 2 :
sử dụng định lý :1/h^2=1/b^2 +1/c^2 => h = BH = 9,6 (cm)
cách 3
Gọi O là giao điểm của AC và BD
Hình thang có 2 đường chéo vuông góc với nhau nên nó là hình thoi
Độ dài 1 cạnh hình thoi
AB = sqrt(OA^2 + OB^2) = sqrt (8^2 + 6^2) = 10 cm
S(hình thoi) = AB*h = AC*BD/2
h = AC*BD(2AB) = 16*12/20 = 9,6 cm
bn chọn cách nào thì chọn nhưng nhớ k mk nha!