Vẽ hình :
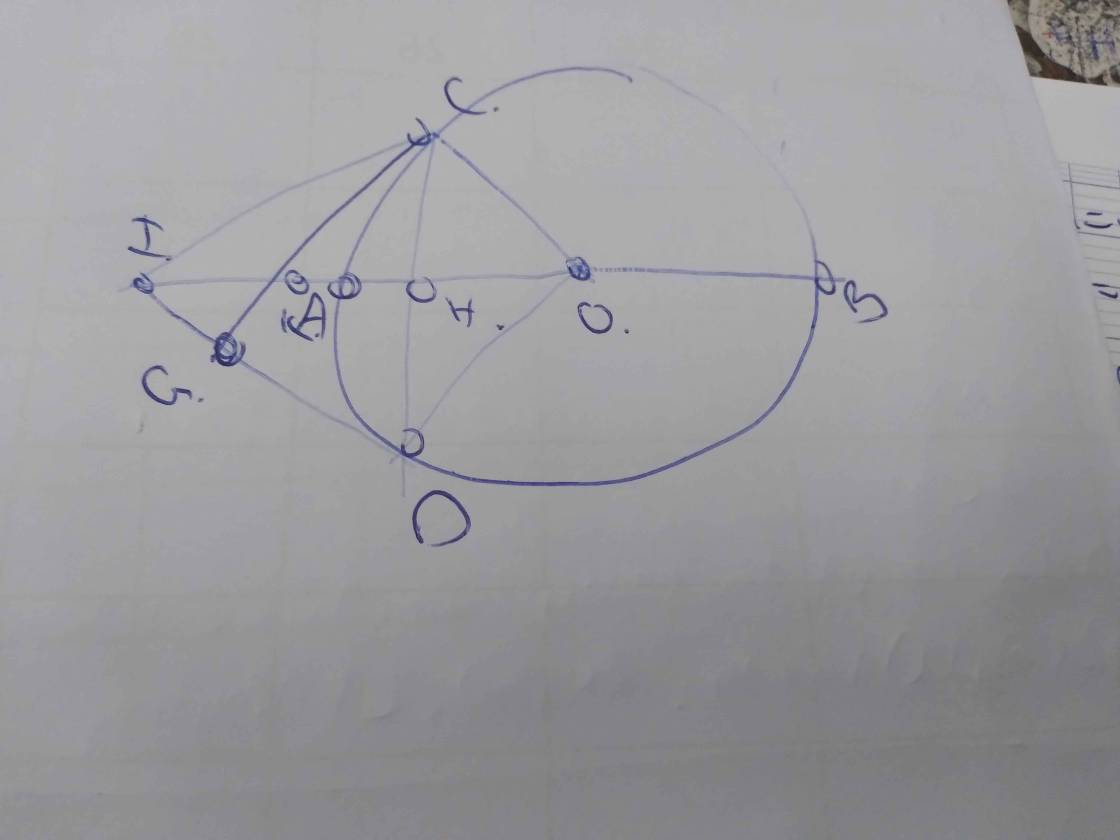
Cho đường tròn ( O ; R ) đường kính AB, dây CD vuông góc với AB tại H ( AH < HB ). Qua C kẻ tiếp tuyến Cx với đường tròn, cắt tia BA tại I. Qua C vẽ tia Cy vuông góc với ID tại G. Gọi K là điểm đối xứng của O qua đoạn CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
8 tháng 9 2023
Đúng(1)
Những câu hỏi liên quan
CM
6 tháng 5 2017
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.
CM
22 tháng 4 2019
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .
CM
15 tháng 2 2018
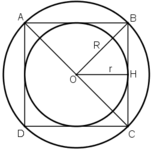
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒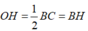 
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.
15 tháng 8 2023
Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
góc ADC=góc AHC=90 độ
=>AHDC nội tiếp
Xét ΔOHC vuông tại H và ΔODA vuông tại D có
OC=OA
góc HOC chung
=>ΔOHC=ΔODA
=>OH=OD
Xét ΔOAC có OH/OA=OD/OC
nên HD//AC
Xét tứ giác AHDC có
HD//AC
góc HAC=góc DCA
=>AHDC là hình thang cân
11 tháng 12 2023
Ta có: ΔOCD cân tại O
mà OM là đường cao(OM\(\perp\)CD tại I)
nên OM là trung trực của CD
12 tháng 4 2017
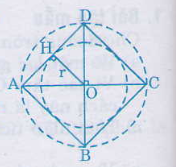
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
CM
12 tháng 4 2018
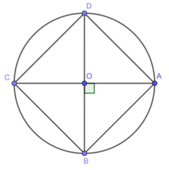
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông