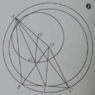
Cho đường tròn tâm O bán kính R trên 1 dây BC cố định. Trên đường tròn lấy 1 điểm A, A không trùng với B và C. Gọi G là trọng tâm của tam giác ABC.
CMR: Khi A di động trên đường tròn tâm O thì G cũng di động trên 1 đường tròn cố định
làm giúp mk nha mk đag cần rất gấp