Một lò xo có độ cứng 25 N/m. Đặt lò xo thẳng đứng. Cố định đầu dưới của lò xo. Đầu trên của lò xo gắn với vật có khối lượng xác định. Lò xo bị nén 4 cm. Tìm khối lượng của vật. Lấy g = 9,8 m/s2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
14 tháng 4 2018
Hệ vật "lò xo - vật - Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.
Chọn mặt phẳng ngang đi qua vị trí A làm mốc tính thế năng trọng trường ( W t = 0) và chọn vị trí lò xo không bị biến dạng làm mốc thế năng đàn hồi ( W đ h = 0). Khi đó cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của động năng W đ thế năng trọng trường W t và thế năng đàn hồi W đ h :
W = W đ + W t + W đ h = m v 2 /2 + mgh + k ∆ l 2 /2
Tại vị trí cân bằng O : hệ vật đứng yên, lò xo bị nén một đoạn ∆ l 0 =10 cm và lực đàn hồi F đ h cân bằng với trọng lực P tác dụng lên vật :
k ∆ l 0 = mg
⇒ k ∆ l 0 = mg ⇒ k = mg/ ∆ l 0 = 8.10/10. 10 - 2 = 800(N/m)
DT
Đỗ Thanh Hải
CTVVIP
8 tháng 3 2021
a) Độ cứng lò xo là : k = \(\dfrac{F}{\left|\Delta l\right|}\) = \(\dfrac{8.10}{0,1}=800\left(\dfrac{N}{m}\right)\)
b) Wđh = \(\dfrac{1}{2}.k.x^2=\dfrac{1}{2.}.800.0,13=52\left(J\right)\)
18 tháng 12 2021
\(F_{đh}=P=10m=10\cdot1=10N\)
\(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{10}{500}=0,02m=2cm\)
\(l=l_0+\Delta l\Rightarrow l_0=l-\Delta l=22-2=20cm\)
VT
4 tháng 9 2018
ü Đáp án D
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 4 cm
+ Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng lên → lực đàn hồi bằng lực phục hồi
- k x = - k Δ l 0 - x ⇒ x = 0 , 5 Δ l 0 = 2 c m
VT
13 tháng 8 2017
Độ biến dạng của lò xo tại vị trí cân bằng
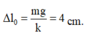
+ Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng lên → lực đàn hồi bằng lực phục hồi
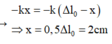
Đáp án D
Ta có: K = 25 N/m; Δl = 4 cm = 0,04 m.
Khi cân bằng ta có
\(\begin{array}{l}P = {F_{dh}} \Leftrightarrow mg = K.\left| {\Delta l} \right|\\ \Rightarrow m = \frac{{K.\left| {\Delta l} \right|}}{g} = \frac{{25.0,04}}{{9,8}} \approx 0,1(kg)\end{array}\)