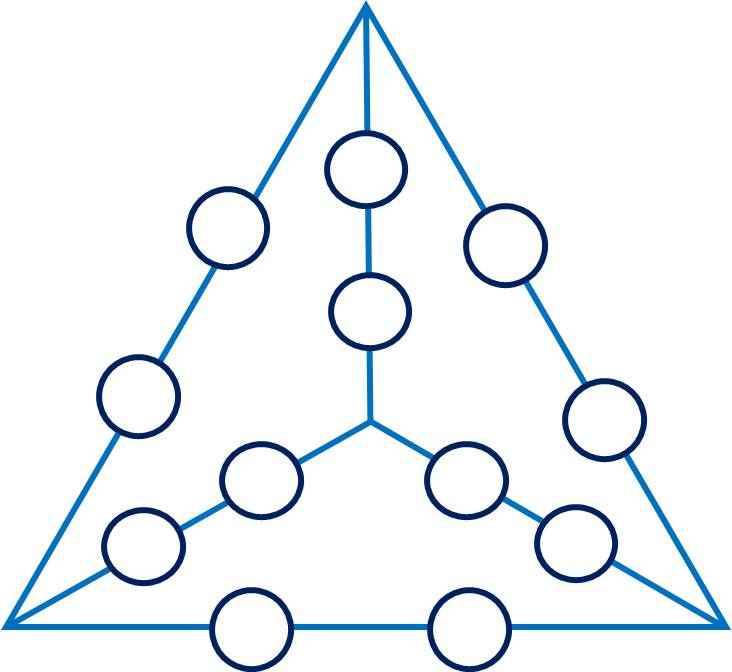
Cho hình tứ diện đều như hình vẽ (góc nhìn từ trên xuống). Mỗi cạnh của tứ diện có hai ô trống tròn.
1. Khi đó tổng mỗi mặt của tứ diện là bao nhiêu?
2. Điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 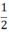 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 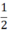 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

Chọn D
Cách 1:
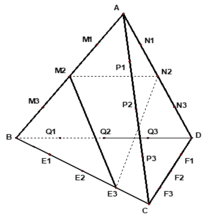
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
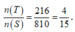
Cách 2: Lưu Thêm
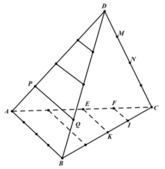
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 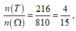

a) Hình này có 4 mặt bên
b) Diện tích của mỗi mặt bên là: \(4.5:2 = 10\) (\(c{m^2}\))
c) Diện tích của tất cả các mặt bên là: \(10.4 = 40\) (\(c{m^2}\))
d) Diện tích đáy là: \(4.4 = 16\) (\(c{m^2}\))

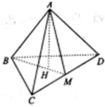
Chọn B.
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có

Cộng lại ta thu được (chú ý rằng)
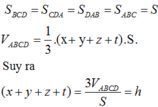
với h là độ dài đường cao của tứ diện đều ABCD. Ta có
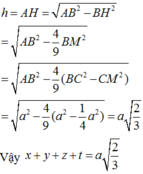

http://www.olm.vn/hoi-dap/question/95083.html
có người làm rùi mà
Để giải bài toán này, ta cần xác định giá trị của các ô trống tròn trên mỗi cạnh của tứ diện đều.
Đầu tiên, ta xác định giá trị của mỗi mặt của tứ diện. Vì tứ diện đều có 4 mặt, ta cần tìm tổng của các ô trống tròn trên mỗi mặt. Do đó, tổng mỗi mặt của tứ diện là tổng giá trị của cả 4 ô trống tròn trên mỗi cạnh.
Để điền số tự nhiên từ 1 đến 12 sao cho tổng mỗi mặt bằng nhau, ta có thể sử dụng phương pháp thử và sai. Ta có thể bắt đầu bằng việc điền các số từ 1 đến 12 vào các ô trống tròn trên mỗi cạnh, và sau đó kiểm tra xem tổng mỗi mặt có bằng nhau hay không.
Dưới đây là một cách điền số để tổng mỗi mặt bằng nhau:
6 1 52 4 3 12
Trong trường hợp này, tổng mỗi mặt sẽ là 1 + 2 + 6 + 3 = 12.
Vì vậy, tổng mỗi mặt của tứ diện đều là 12.