tìm x: |3x-2/5| = 1/35 + 18/7
giúp mik vs ạ:,,
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1
\(0,3:2,5=3:25\)
\(4\dfrac{2}{5}:1\dfrac{1}{3}=\dfrac{22}{5}:\dfrac{4}{3}=33:10\)
\(-3,2:1\dfrac{2}{7}=\dfrac{-16}{5}:\dfrac{9}{7}=112:45\)
SV
Sinh Viên NEU
CTVVIP
9 tháng 1
a
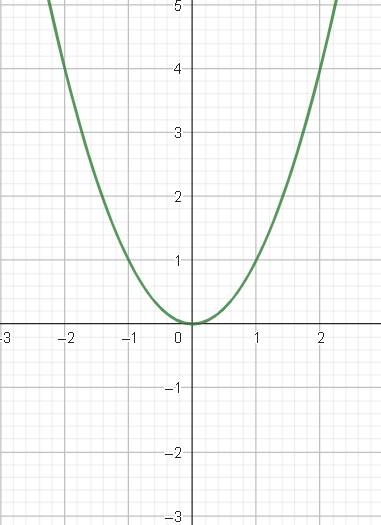
b) Xét phương trình hoành độ giao điểm của (P) và (d'):
\(x^2=x-2m+1\)
\(\Leftrightarrow x^2-x+2m-1=0\)
\(\Delta=\left(-1\right)^2-4.1.\left(2m-1\right)=5-8m\)
Để (d') cắt (P) tại 2 điểm phân biệt: \(\Delta>0\Leftrightarrow5>8m\Leftrightarrow m< \dfrac{5}{8}\)
Theo định lí Vi-et:
\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1.x_2=2m-1\end{matrix}\right.\)
Theo bài: \(x_1^2+x_2^2=7\)
\(\Leftrightarrow x_1^2+2x_1x_2+x_2^2-2x_1x_2=7\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=7\)
\(\Leftrightarrow1^2-2\left(2m-1\right)=7\)
\(\Leftrightarrow1-4m+2=7\)
\(\Leftrightarrow-4m=4\Leftrightarrow m=-1\left(tmm< \dfrac{5}{8}\right)\)
Vậy m = -1 là giá trị cần tìm
H9
HT.Phong (9A5)
CTVHS
9 tháng 1
a) 
b) Đường thẳng (d') cắt (P) ta có phương trình hoành độ giao điểm là:
\(x^2=x-2m+1\)
\(\Leftrightarrow x^2-x+2m-1=0\)
\(\Delta=\left(-1\right)^2-4\cdot1\cdot\left(2m-1\right)=1-8m+4=-8m+5\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{1+\sqrt{5-8m}}{2}\\x_2=\dfrac{1-\sqrt{5-8m}}{2}\end{matrix}\right.\left(đk:m\le\dfrac{5}{8}\right)\)
Mà: \(x^2_1+x^2_2=7\)
\(\Leftrightarrow\left(\dfrac{1+\sqrt{5-8m}}{2}\right)^2+\left(\dfrac{1-\sqrt{5-8m}}{2}\right)^2=7\)
\(\Leftrightarrow\dfrac{1+2\sqrt{5-8m}+5-8m}{4}+\dfrac{1-2\sqrt{5-8m}+5-8m}{4}=7\)
\(\Leftrightarrow\dfrac{6+2\sqrt{5-8m}-8m+6-2\sqrt{5-8m}-8m}{4}=7\)
\(\Leftrightarrow12-16m=28\)
\(\Leftrightarrow-16m=16\)
\(\Leftrightarrow m=-1\left(tm\right)\)
Vậy: ....
NT
1
12 tháng 9 2021
\(A=-x\left(x-6\right)+7\)
\(=-x^2+6x+7\)
\(=-\left(x^2-6x-7\right)\)
\(=-\left(x^2-6x+9-16\right)\)
\(=-\left(x-3\right)^2+16\le16\forall x\)
Dấu '=' xảy ra khi x=3
1 tháng 1 2022
-x-2/3=-6/7
-x =-6/7+2/3
-x =-18/21+14/21
-x =-4/21
=> x=4/21
C
7 tháng 4 2022
4/9-5/18 = 8/18 - 5/18 = 3/18 = 1/6
3/5x5/7 = 3/7
4/7:2/7 = 4/7 x 7/2 = 2
VQ
7 tháng 4 2022
4/9-5/18= 8/18 - 5/18 = 3/18 = 1/6
3/5x5/7=15/35 = 3/7
4/7:2/7=4/7 x 7/2 = 4/2 = 2
23 tháng 6 2023
a: =>2x^2-2x+2x-2-2x^2-x-4x-2=0
=>-5x-4=0
=>x=-4/5
b: =>6x^2-9x+2x-3-6x^2-12x=16
=>-19x=19
=>x=-1
c: =>48x^2-12x-20x+5+3x-48x^2-7+112x=81
=>83x=83
=>x=1
KG
1
26 tháng 7 2023
a: =>(x-5)(x+5)+(x-5)(3x-15)=0
=>(x-5)(x+5+3x-15)=0
=>(x-5)(4x-10)=0
=>x=5 hoặc x=5/2
c: =>x^3-3x^2+2x^2-6x-8x+24=0
=>(x-3)(x^2+2x-8)=0
=>(x-3)(x+4)(x-2)=0
=>\(x\in\left\{3;-4;2\right\}\)
20 tháng 5 2023
`A(x)=-2x^2+5x+7=0`
`=> -(2x^2-5x+7)=0`
`=> -(2x^2-2x-7x+7)=0`
`=> -[(2x^2-2x)-(7x-7)]=0`
`=> -[2x(x-1)-7(x-1)]=0`
`=> -[(2x-7)(x-1)]=0`
`=> -(2x-7)(x-1)=0`
`=> (2x-7)(x+1)=0`
`=>`\(\left[{}\begin{matrix}2x-7=0\\x+1=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2x=7\\x=-1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-1\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={7/2; -1}.`
TC
19 tháng 4 2022
a)\(3x-\dfrac{2}{5}=0=>3x=\dfrac{2}{5}=>x=\dfrac{2}{15}\)
b)\(\left(x-3\right)\left(2x+8\right)=0=>\left[{}\begin{matrix}x-3=0\\2x=-8\end{matrix}\right.=>\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
c)\(3x^2-x-4=0=>3x^2+3x-4x-4=0=>\left(3x-4\right)\left(x+1\right)=0\)
\(=>\left[{}\begin{matrix}3x=4\\x+1=0\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=-1\end{matrix}\right.\)
=>|3x-2/5|=1/35+90/35=91/35
=>3x-2/5=91/35 hoặc 3x-2/5=-91/35
=>3x-2/5=13/5 hoặc 3x-2/5=-13/5
=>3x=15/5=3 hoặc 3x=-11/5
=>x=-11/5 hoặc x=1
Lời giải:
$|3x-\frac{2}{5}|=\frac{1}{35}+\frac{18}{7}=\frac{13}{5}$
$\Rightarrow 3x-\frac{2}{5}=\frac{13}{5}$ hoặc $3x-\frac{2}{5}=\frac{-13}{5}$
$\Rightarrow 3x=3$ hoặc $3x=\frac{-11}{5}$
$\Rightarrow x=1$ hoặc $x=\frac{-11}{15}$