Hai tàu rời cảng cùng thời điểm . Tàu thứ nhất , đi theo hướng N 15 độ W với vận tốc 25 hải lý/h . Tàu thứ hai đi theo hướng N 32 độ E với vận tốc 20 hải lí/h . Sau 2 giờ , hai chiếc xe cách nhau bao nhiêu xa ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
26 tháng 2 2021
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có AB=40,AC=30 và ˆA=600.
Áp dụng định lí côsin vào tam giác ABC, ta có
a2=b2+c2−2bccosA=302+402−2.30.40.cos600=900+1600−1200=1300
Vậy BC=√1300≈36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.
CM
5 tháng 6 2019
Chọn C.
Sau 2h quãng đường tàu thứ nhất chạy được là: S1 = 30.2 = 60km
Sau 2h quãng đường tàu thứ hai chạy được là: S2= 40.2 = 80 km
Suy ra sau 2h hai tàu cách nhau là:
24 tháng 9 2023
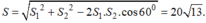
Tham khảo:
Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu thứ hai sau 2,5 giờ.
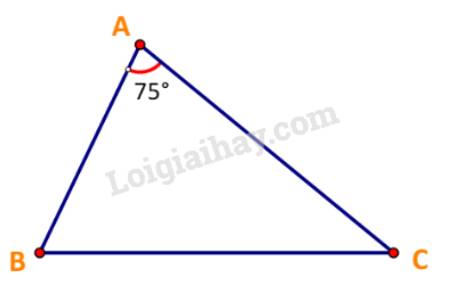
Sau 2,5 giờ:
Quãng đường tàu thứ nhất đi được là: AB = 8.2,5 = 20 (hải lí)
Quãng đường tàu thứ hai đi được là: AC = 12.2,5 = 30 (hải lí)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\(\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} - 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}\)
Vậy hai tàu cách nhau 31,5 hải lí.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
Sau 2h tàu thứ nhất ở vị trí B cách A là: \(2.30=60\left(km\right)\)
Tàu thứ 2 ở vị trí C cách A là: \(2.40=80\left(km\right)\)
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos60^0}=20\sqrt{13}\approx72,1\left(km\right)\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
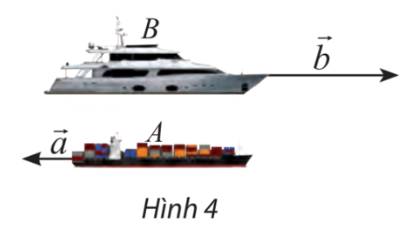
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)
17 tháng 10 2021
Đổi: 6 giờ 30ph = 6,5h, 15m/s=54km/h
Gọi t là thời gian 2 xe gặp nhau
\(\Rightarrow\left\{{}\begin{matrix}S_1=54t\left(km\right)\\S_2=32t\left(km\right)\end{matrix}\right.\)
\(\Rightarrow S_1+S_2=54t+32t=86t=270\)
\(\Rightarrow t=\dfrac{135}{43}\left(h\right)\)
2 xe gặp nhau lúc: \(6,5+\dfrac{135}{43}=\approx9,6\left(h\right)\)
Vị trí 2 xe gặp nhau cách A: \(S_1=54.\dfrac{135}{43}\approx170\left(km\right)\)
Vị trí 2 xe gặp nhau cách B: \(S_2=\dfrac{32.135}{43}\approx100\left(km\right)\)
17 tháng 10 2021
bn lên đổi sang thành 258km giả sử AB=258km vì 2 xe gặp nhau cùng thời điểm lên sẽ cùng 1 thời gian và gọi là x (h) ta có 15m/s=54km/h
suy ra : 258-54x=32x ==>x=3h vậy hai xe gặp nhau vào lúc 9h30p cách A 162km và cách B 96km
VT
21 tháng 7 2019
Đáp án B
Gọi hai tàu hoả là (1) và (2)
Khi hai tàu gặp nhau thì thời gian đi được của chúng là:
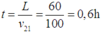
Tổng quãng đường mà con chim đã bay được là: s = vchimt = 30.0,6 = 18 km
8 tháng 8 2021
\(=>S1=60t\left(km\right)\)
\(=>S2=40t\left(km\right)\)
\(=>S1+S2=60t+40t=100=>t=1h\)
sau 1h 2 xe gặp nhau
Sau 2 giờ, tàu thứ nhất đã đi được `25.2 = 50` hải lý.
Sau 2 giờ, tàu thứ hai đã đi được `20.2 = 40` hải lý.
Với a = `50` hải lý, b = `40` hải lý và `C = 180° - (15° + 32°) = 133°`, ta có:
`c^2 = 50^2 + 40^2 - 2.50.40.cos(133°)`
=> `c^2 ≈ 2500 + 1600 - 4000.(-0.6428) ≈ 4107.14`
Vậy, khoảng cách giữa hai tàu sau 2 giờ là:
`c ≈ √4107.14 ≈ 64,07 hải lý`
hi