D=1/1.5+1/5.9+...+1/41.45 Mn lm nhanh giúp mik vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{1.5}+\frac{1}{5.9}+\frac{1}{9.13}+\frac{1}{13.17}+...+\frac{1}{41.45}\)
\(=\frac{1}{4}.\left(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+...+\frac{1}{41}-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\left(1-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\frac{44}{45}\)
\(=\frac{11}{45}\)
Đặt \(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\) là A.
Ta có:
\(A=\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\)
\(4A=4\left(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\right)\)
\(4A=\frac{4}{1\cdot5}+\frac{4}{5\cdot9}+\frac{4}{9\cdot13}+\frac{4}{13\cdot17}+...+\frac{4}{41\cdot45}\)
\(4A=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\frac{1}{13}-\frac{1}{17}+...+\frac{1}{41}-\frac{1}{45}\)
\(4A=1-\frac{1}{45}\)
\(4A=\frac{44}{45}\)
\(A=\frac{44}{45}:4\)
\(A=\frac{11}{45}\)
Vậy \(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}=\frac{11}{45}\)

\(\dfrac{1}{4}+\dfrac{1}{3}\times X=\dfrac{1}{2}\\ \dfrac{1}{3}\times X=\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1}{4}\\ X=\dfrac{1}{4}:\dfrac{1}{3}=\dfrac{1}{4}\times3=\dfrac{3}{4}\)
14+13×�=1213×�=12−14=14�=14:13=14×3=3441+31×X=2131×X=21−41=41X=41:31=41×3=43

\(\dfrac{3}{4}\times X-1=\dfrac{1}{2}\times X\\ \dfrac{3}{4}\times X-\dfrac{1}{2}\times X=1\\ \left(\dfrac{3}{4}-\dfrac{1}{2}\right)\times X=1\\ \dfrac{1}{4}\times X=1\\ X=1:\dfrac{1}{4}\\ X=4\)
\(\dfrac{3}{4}\times x-1=\dfrac{1}{2}\times x\\ \dfrac{3}{4}\times x-\dfrac{1}{2}\times x=1\\ x\times\left(\dfrac{3}{4}-\dfrac{1}{2}\right)=1\\ x\times\dfrac{1}{4}=1\\ x=1:\dfrac{1}{4}\\x=4\)

$#trúc$
`4/(1.5) + 4/(5.9) + 4/(9.13) + .... + 4/(2013 . 2017)`
=`1 - 1/5 + 1/5 - 1/9 + 1/9 - 1/13 + ... + 1/2013 - 1/2017`
= `1 - 1/2017`
= `2017/2017 - 1/2017`
= `2016/2017`

\(A=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{420}\\ \Rightarrow A=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{20\times21}\\ \Rightarrow A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{20}-\dfrac{1}{21}\\\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{20}=\dfrac{9}{20}\)
Sau khi rút gọn phải còn:
\(A=\dfrac{1}{2}-\dfrac{1}{21}\) (chứ anh)
\(A=\dfrac{19}{42}\)

\(B=\frac{1}{1.5}+\frac{1}{5.9}+...+\frac{1}{41.45}\)
\(4B=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+...+\frac{1}{41}-\frac{1}{45}\)
\(4B=\frac{44}{45}\)
\(B=\frac{11}{45}\)
\(B=\frac{1}{1.5}+\frac{1}{5.9}+...+\frac{1}{41.45}\)
\(=\frac{1}{4}.\left(\frac{4}{1.5}+\frac{4}{5.9}+...+\frac{4}{41.45}\right)\)
\(=\frac{1}{4}.\left(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+...+\frac{1}{41}-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\left(1-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\frac{44}{45}\)
\(=\frac{11}{45}\)

\(M=\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=\dfrac{2}{\left|2-\sqrt{5}\right|}-\dfrac{2}{\left|2+\sqrt{5}\right|}\)
\(=\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{\sqrt{5}+2}=\dfrac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
\(=\dfrac{8}{1}=8\)
Lm ơn giúp mik đii mà mik bt ơn bn đó nhiều lắm . Mik đang rất cần

1) \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)
2) \(\left(2x-3\right)^2=4x^2-12x+9\)
\(\left(3x-2\right)^2=9x^2-12x+4\)
\(\left(2x-5\right)^2=4x^2-20x+25\)
\(\left(2x-\dfrac{1}{3}\right)^2=4x^2-\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x-\dfrac{1}{3}\right)^2=9x^2-2x+\dfrac{1}{9}\)
3) \(\left(2x-3\right)\left(2x+3\right)=4x^2-9\)
\(\left(3x-4\right)\left(3x+4\right)=9x^2-16\)
\(\left(2x-5\right)\left(2x+5\right)=4x^2-25\)
\(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)=x^2-\dfrac{1}{4}\)
\(\left(2x-\dfrac{1}{3}\right)\left(2x+\dfrac{1}{3}\right)=4x^2-\dfrac{1}{9}\)
1: \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)

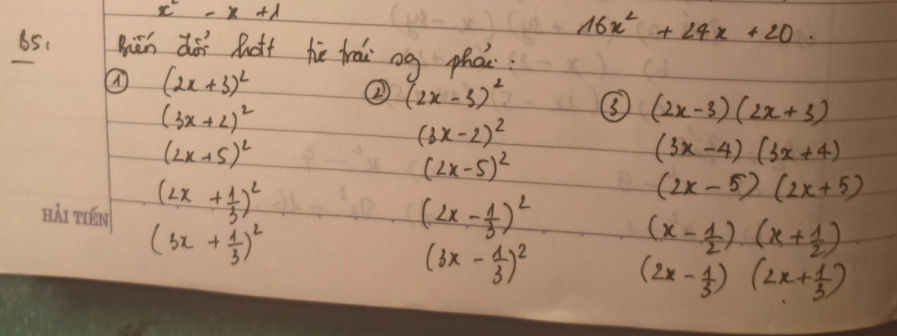
D=1/1.5+1/5.9+...+1/41.45
4D=4/1.5+4/5.9+...+4/41.45
4D=1-1/5+1/5-1/9+...+1/41-1/45
4D=1-1/45
D=44/45:4=11/45