mọi người ơi giúp mình bài 3 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


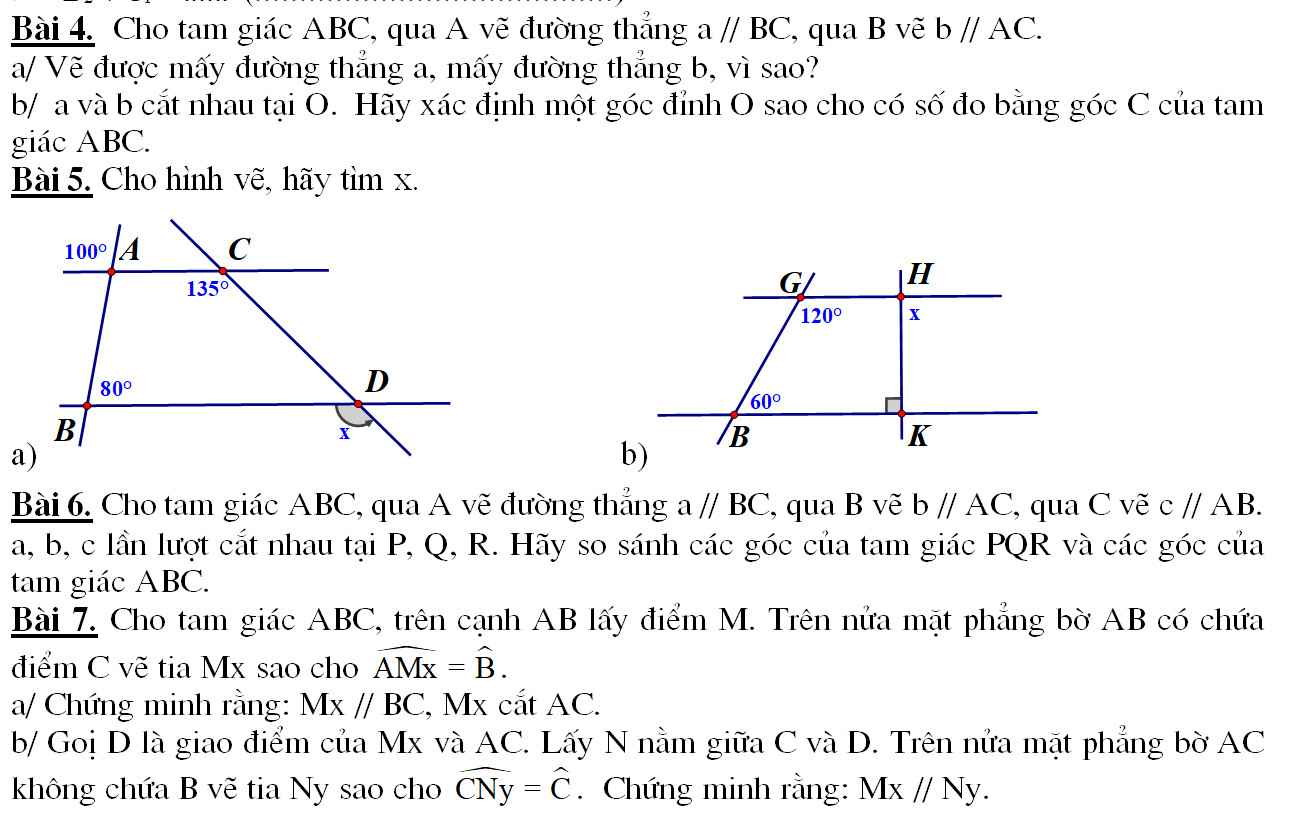
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)

4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c

b: \(\Leftrightarrow\left(2x-7\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{3}\end{matrix}\right.\)

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật






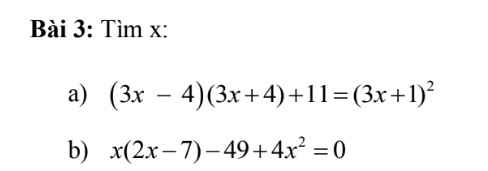


Cấu trúc mạch cho câu (a), (b): \(R_1\text{ nt }R_{BC}\text{ nt }\left[Đ\left|\right|\left(R_{AC}\text{ nt }R_2\right)\right]\)
(a) Theo đề bài: \(R_{AC}=2R_{BC}\Rightarrow R_{AC}=\dfrac{2}{3}R_0;R_{BC}=\dfrac{1}{3}R_0\)
Điện trở của bóng đèn: \(R_Đ=\dfrac{U_{đm}^2}{P_{đm}}=\dfrac{1,5^2}{0,75}=3\left(\Omega\right)\)
Điện trở tương đương của đoạn mạch:
\(R=R_1+R_{BC}+\dfrac{R_Đ\left(R_{AC}+R_2\right)}{R_Đ+R_{AC}+R_2}\)
\(=2+\dfrac{1}{3}R_0+\dfrac{3\left(\dfrac{2}{3}R_0+2\right)}{3+\dfrac{2}{3}R_0+2}\)
\(=\dfrac{2R_0^2+45R_0+144}{3\left(15+2R_0\right)}\)
Cường độ dòng điện qua mạch chính:
\(I=\dfrac{U}{R}=\dfrac{U}{\dfrac{2R_0^2+45R_0+144}{3\left(15+2R_0\right)}}=\dfrac{3U\left(15+2R_0\right)}{2R_0^2+45R_0+144}\)
Hiệu điện thế hai đầu đèn:
\(U_Đ=I\cdot\dfrac{R_Đ\left(R_{AC}+R_2\right)}{R_Đ+R_{AC}+R_2}=\dfrac{3U\left(15+2R_0\right)}{2R_0^2+45R_0+144}\cdot\dfrac{3\left(\dfrac{2}{3}R_0+2\right)}{3+\dfrac{2}{3}R_0+2}=\dfrac{9U\left(2R_0+6\right)}{2R_0^2+45R_0+144}\)Do đèn sáng bình thường nên:
\(U_Đ=U_{đm}\Leftrightarrow\dfrac{9U\left(2R_0+6\right)}{2R_0^2+45R_0+144}=1,5=\dfrac{3}{2}\left(1\right)\)
Số chỉ của Ampe kế: \(I_A=\dfrac{R_Đ}{R_Đ+R_{AC}+R_2}I=\dfrac{3}{3+\dfrac{2}{3}R_0+2}\cdot\dfrac{3U\left(15+2R_0\right)}{2R_0^2+45R_0+144}=\dfrac{27U}{2R_0^2+45R_0+144}=0,25\left(2\right)\)
Từ \(\left(2\right)\Rightarrow108U=2R_0^2+45R_0+144\)
Thay vào \(\left(1\right)\Rightarrow\dfrac{9U\left(2R_0+6\right)}{108U}=\dfrac{3}{2}\Leftrightarrow R_0=6\left(\Omega\right)\)
Thay lại vào \(\left(2\right)\Rightarrow U=4,5\left(V\right)\)
(b) Đặt: \(R_{AC}=x\left(0\le x\le R_0=6\right)\Rightarrow R_{CB}=6-x\)
Điện trở tương đương của đoạn mạch:
\(R=R_1+R_{CB}+\dfrac{R_Đ\left(R_{AC}+R_2\right)}{R_Đ+R_{AC}+R_2}=2+6-x+\dfrac{3\left(x+2\right)}{3+x+2}\)
\(=\dfrac{-x^2+6x+46}{x+5}\)
Cường độ dòng điện qua mạch chính: \(I=\dfrac{U}{R}=\dfrac{4,5}{\dfrac{-x^2+6x+46}{x+5}}=\dfrac{9\left(x+5\right)}{2\left(-x^2+6x+46\right)}\)
Hiệu điện thế hai đầu đèn:
\(U_Đ=I\cdot\dfrac{R_Đ\left(R_{AC}+R_2\right)}{R_Đ+R_{AC}+R_2}=\dfrac{9\left(x+5\right)}{2\left(-x^2+6x+46\right)}\cdot\dfrac{3\left(x+2\right)}{3+x+2}=\dfrac{27\left(x+2\right)}{2\left(-x^2+6x+46\right)}\)
Số chỉ của Ampe kế: \(I_A=\dfrac{R_Đ}{R_Đ+R_{AC}+R_2}I=\dfrac{3}{3+x+2}\cdot\dfrac{9\left(x+5\right)}{2\left(-x^2+6x+46\right)}=\dfrac{27}{2\left(-x^2+6x+46\right)}\)
\(I_A\) nhỏ nhất khi \(-x^2+6x+46\) lớn nhất.
Ta có: \(-x^2+6x+46=-\left(x-3\right)^2+55\le55\)
\(\Rightarrow Max\left(-x^2+6x+46\right)=55\) khi \(x=R_{AC}=3\left(\Omega\right)\)
\(\Rightarrow MinI_A=\dfrac{27}{2\cdot55}=\dfrac{27}{100}\left(A\right)\)
Khi đó: \(U_Đ=\dfrac{54}{55}\left(V\right)< U_{đm}\) nên đèn sáng yếu hơn bình thường.
Vậy: \(MinI_A=\dfrac{27}{100}=0,27\left(A\right)\Leftrightarrow R_{AC}=3\left(\Omega\right)\), đèn lúc này sáng yếu.
(c) Cấu trúc mạch: \(R_1\text{ nt }R_{BC}\)
Lúc này, số chỉ của Ampe kế là cường độ dòng điện qua mạch chính.
\(I_A\) nhỏ nhất, tức cường độ dòng điện qua mạch chính nhỏ nhất khi điện trở tương đương của mạch lớn nhất, suy ra \(R_{BC}\) lớn nhất hay \(R_{BC}=R_0=6\left(\Omega\right)\).
Số chỉ của Ampe kế lúc này là:
\(I_A=I=\dfrac{U}{R_1+R_{BC}}=\dfrac{4,5}{2+6}=0,5625\left(A\right)\)