Cho hình bình hành ABCD (AB>AD). Tia phân giác của góc CAD cắt DC tại M, tia phân giác của góc ACB cắt AB tại N.
a) Chứng minh AN // CN
b) Tứ giác AMCN là hình gì?
c) Lấy các điểm E,F lần lượt trên cạnh BC, DA sao cho BE=DF. Chứng minh ME//FN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2023
a: Xét ΔADN và ΔCBM có
góc A=góc C
AD=CB
góc ADN=góc CBM
=>ΔADN=ΔCBM
b: ΔADN=ΔCBM
=>AN=CM
AN+NB=AB
CM+MD=CD
mà AN=CM và AB=CD
nên NB=MD
mà NB//MD
nên NBMD là hình bình hành
c: Xét tứ giác AMCN có
AN//CM
AN=CM
=>AMCN là hình bình hành
22 tháng 10 2023
Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
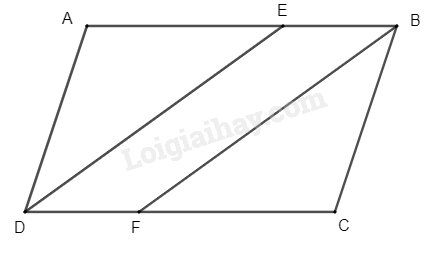
a) Vì \(DE\), \(BF\) là phân giác (gt)
Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\); \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)
Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)
Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DE\) // \(BF\)
b) Xét tứ giác \(DEBF\) ta có:
\(DE\) // \(BF\) (cmt)
\(BE\) // \(DF\) (do \(AB\) // \(CD\))
Suy ra \(DEBF\) là hình bình hành
27 tháng 7 2021
Ta có: \(\widehat{DEA}=\widehat{EDC}\)(hai góc so le trong, AE//DC)
mà \(\widehat{EDC}=\widehat{ADE}\)(DE là tia phân giác của \(\widehat{ADC}\))
nên \(\widehat{ADE}=\widehat{AED}\)
Xét ΔAED có \(\widehat{ADE}=\widehat{AED}\)(cmt)
nên ΔAED cân tại A(Định lí đảo của tam giác cân)
Suy ra: AD=AE(đpcm)