Tìm nghiệm nguyên của phương trình để phương trình là số chính phương
x4+x3+x2+x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.

1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m

\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài

Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).

Đáp án C
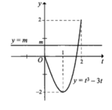
Vẽ đồ thị hàm số y = x 3 − 3 x 2 + 1

Để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 thì đường thẳng y=m cắt đồ thị hàm số y = x 3 − 3 x 2 + 1 tại ba điểm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 ⇔ − 3 < m < − 1.

Đáp án A
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()
Phương trình thì phải có hai vế chứ
không nhìn đề ak.đa bảo là số chính phương thì vế trái của nó là 1 sô chính phương hay nói cách khác là =k2