mọi người làm giúp e bài 1 nhé đc bài 2 thì càng tốt ạ. cảm ơn mọi người
K
Khách
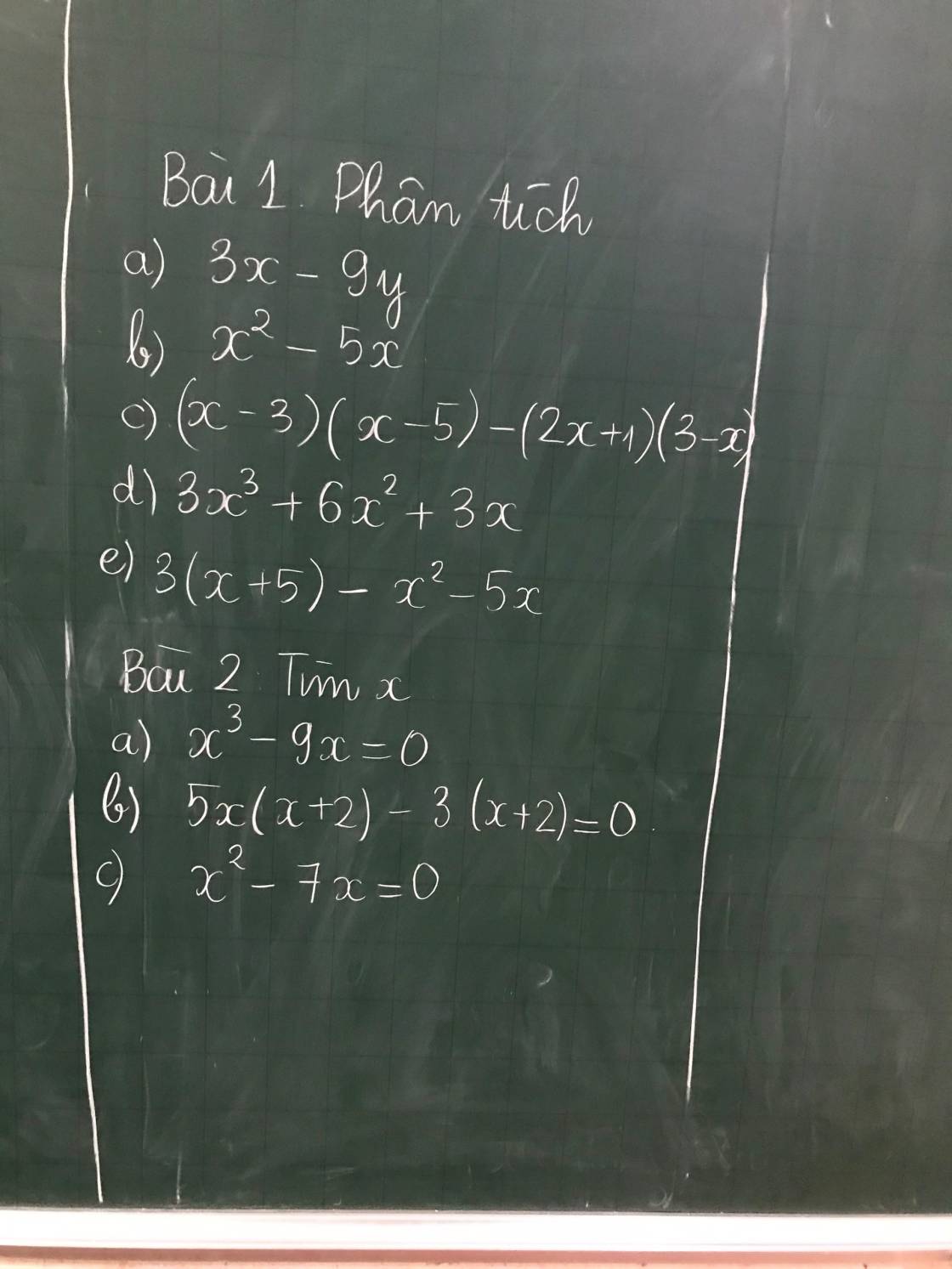
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PD
2
Những câu hỏi liên quan
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
NV
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
LY
2
BT
Bùi Thế Nghị
Giáo viên
20 tháng 7 2021
Quy đổi hỗn hợp X thành \(\left\{{}\begin{matrix}Ba\\Na\\O\end{matrix}\right.\) với nBa = x mol, nNa = y mol và nO = z mol
nH2 = 1,12 :22,4 = 0,05 mol
\(\left\{{}\begin{matrix}Ba\\Na\\O\end{matrix}\right.\) + H2O → \(\left\{{}\begin{matrix}Ba\left(OH\right)_2\\NaOH\end{matrix}\right.\) + H2
Ta có nBa(OH)2 = 20,52: 171 = 0,12 mol
Bảo toàn nguyên tố Ba => x = 0,12 mol
Áp dụng ĐLBT electron và BTKL ta có \(\left\{{}\begin{matrix}y+0,12.2=2z+0,05.2\\0,12.137+23y+16z=21,9\end{matrix}\right.\)
=> y = 0,14 và z = 0,14
a) BTKL => nNaOH = nNa = 0,14 mol
b) nOH- trong dung dịch Y = 0,12.2 +0,14 = 0,38 mol
nCO2 = 6,72:22,4 = 0,3 mol
Ta có \(\dfrac{nOH^-}{nCO_2}\) = 1,26 => tạo 2 muối HCO3- và CO32-
CO2 + OH- → HCO3-
0,3 0,38(dư) 0,3
OH- + HCO3- → CO32- + H2O
0,08 0,3 0,08
CO32- + Ba2+ → BaCO3
0,08 0,12 ---> 0,08
Vậy mBaCO3 = m kết tủa = 0,08.197 = 15,76 gam
BT
Bùi Thế Nghị
Giáo viên
20 tháng 7 2021
Cách 2
\(\left[{}\begin{matrix}Na\\Ba\\Na_2O\\BaO\end{matrix}\right.\) + H2O → \(\left\{{}\begin{matrix}Ba\left(OH\right)_2\\NaOH\left(xmol\right)\end{matrix}\right.\) + H2
Tổng số mol H sau phản ứng = 2nBa(OH)2 + nNaOH + 0,05.2 = (0,34 +x) mol
=> nH2O phản ứng = 0,17 + 0,5x mol
Áp dụng ĐLBT khối lượng => 21,9 + (0,17 + 0,5x).18 = 20,52 + 40x + 0,05.2
=> x = 0,14
Đến đây em giải tiếp tương tự cách 1
DD
Đoàn Đức Hà
Giáo viên
19 tháng 7 2021
Trả lời bằng Tiếng Việt nhé.
Bài 1.
Nếu đi với vận tốc \(50m/min\)thì sẽ đến trường muộn hơn đi với vận tốc \(60m/min\)số phút là:
\(2+1=3\)(phút)
Mỗi mét đi với vận tốc \(50m/min\)hết số phút là:
\(1\div50=\frac{1}{50}\)(phút)
Mỗi mét đi với vận tốc \(60m/min\)hết số phút là:
\(1\div60=\frac{1}{60}\)(phút)
Mỗi mét đi với vận tốc \(60m/min\)nhanh hơn mỗi mét đi với vận tốc \(50m/min\)số phút là:
\(\frac{1}{50}-\frac{1}{60}=\frac{1}{300}\)(phút)
Quãng đường từ nhà đến trường dài:
\(3\div\frac{1}{300}=900\left(m\right)\)
DD
Đoàn Đức Hà
Giáo viên
19 tháng 7 2021
Bài 2.
Để lấy được ít nhất \(20\)cái bút cùng màu thì ta cần lấy ra hết số bút có ít hơn \(20\)cái, số bút có từ \(20\)cái trở lên ta lấy mỗi loại \(19\)cái, sau đó ta lấy thêm \(1\)cái nữa thì chắc chẵn sẽ được ít nhất \(20\)cái bút có cùng màu.
Số bút ít nhất cần lấy ra là:
\(8+12+19+19+1=59\)(cái)
MT
1
11 tháng 7 2016
= x3 + 33 -x(x2 -1) -27 =0 ( tổng các lập phuong)
x =0
CX100%
2 tháng 3 2021
\(\Rightarrow A=\frac{6n+2-5}{3n+1}=\frac{2\left(3n+1\right)}{3n+1}-\frac{5}{3n+1}\)=\(2-\frac{5}{3n+1}\)
Để A có giá trị nguyên \(\Leftrightarrow5⋮3n+1\Rightarrow3n+1\in\left\{-5;-1;1;5\right\}\)
\(\Rightarrow3n\in\left\{-6;-2;0;4\right\}\Rightarrow n\in\left\{-2;-\frac{2}{3};0;\frac{4}{3}\right\}\) Mà n \(\in Z\)
\(\Rightarrow n\in\left\{-2;0\right\}\)
QA
2 tháng 3 2021
Trả lời:
Ta có: \(\frac{6n-3}{3n+1}=\frac{2\left(3n+1\right)-5}{3n+1}=\frac{2\left(3n+1\right)}{3n+1}-\frac{5}{3n+1}=2-\frac{5}{3n+1}\)
Để A là số nguyên thì \(\frac{5}{3n+1}\)là số nguyên
=> \(5⋮3n+1\) hay \(3n+1\inƯ\left(5\right)\)\(=\left\{\pm1;\pm5\right\}\)
Ta có bảng sau:
| 3n+1 | 1 | -1 | 5 | -5 |
| 3n | 0 | -2 | 4 | -6 |
| n | 0 | \(\frac{-2}{3}\)(loại) | \(\frac{4}{3}\)(loại) | -2 |
Vậy n \(\in\){ 0 ; -2 } thì A có giá trị nguyên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 7 2023
Em dùng công thức toán học hoặc viết ra giấy, chụp ảnh rồi up lên chứ thế này cô không đúng đề bài để giúp em được.
\(Bài.1:\\ a,3x-9y=3\left(x-3y\right)\\ b,x^2-5x=x\left(x-5\right)\\ c,\left(x-3\right)\left(x-5\right)-\left(2x+1\right)\left(3-x\right)=\left(x-3\right)\left(x-5\right)+\left(x-3\right)\left(2x+1\right)\\ =\left(x-3\right)\left(x-5+2x+1\right)=\left(x-3\right)\left(3x-4\right)\\ d,3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\\ e,3\left(x+5\right)-x^2-5x=3\left(x+5\right)-x\left(x+5\right)\\ =\left(x+5\right)\left(3-x\right)\)
\(Bài.2:\\ a,x^3-9x=0\\ \Leftrightarrow x.\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\\ b,5x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-2\end{matrix}\right.\\ c,x^2-7x=0\\ \Leftrightarrow x\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)