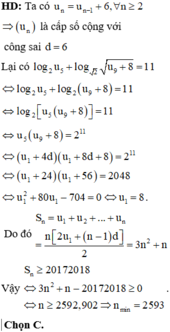tìm số tự nhiên n sao cho Sn=n^2 -2017n+10 với Sn là tổng các chữ số của n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TS
2
27 tháng 12 2017
\(S_{\left(n\right)}=n^2-2017n+10\)
Vì S(n) là tổng các chữ số \(\Rightarrow S_{\left(n\right)}>0\)
hay \(n^2-2017n+10\)\(>0\)
\(\Rightarrow\)\(\frac{n^2+10}{n}\)\(>2017\)
\(\Rightarrow\)\(n+\frac{10}{n}\)\(>2017\)
\(\Rightarrow n\ge2017^{\left(1\right)}\)
Có :\(S_{\left(n\right)}< n\)
hay \(n^2-2017n+10< n\)
\(\Rightarrow n^2+10>2017n+n\)
\(\Rightarrow n^2+10< 2018n\)
\(\Rightarrow\frac{n^2+10}{n}< 2018\)
\(\Rightarrow\frac{10}{n}+n< 2018\)
\(\Rightarrow n< 2018^{\left(2\right)}\)
Từ (1) và (2)
\(\Rightarrow n=2017\)
Ai thấy đk thì k cho mk 1 cái, mk cảm ơn!
NC
2
Q
19 tháng 6 2017
Ta có 3 trường hợp:
+) Nếu \(1\le n\le2016\) thì ta có:
\(S_{\left(n\right)}=n^2-2017n+10< n^2-2017n+2016\)
\(=\left(n-1\right)\left(n-2016\right)\ge0\) (loại)
+) Nếu \(n=2017\) thì ta có:
\(S_{\left(n\right)}=S_{\left(2017\right)}=10=n^2-2017n+10\) (nhận)
+) Nếu \(n>2017\) thì ta có:
\(S_{\left(n\right)}=n^2-2017n+10>n\left(n-2017\right)>n\) (loại)
Vậy \(n=2017\)
17 tháng 8 2023
a: S8={1;2;4;8}
S9={1;3;9}
S12={1;2;3;4;6;12}
b: M chia hết cho n
=>\(n\inƯ\left(m\right)\)
=>Ước của n chắc chắn sẽ là ước của m
=>\(S_n\subset S_M\)
c: \(S_n\subset S_m\)
=>Ước của n là ước của m
=>n là ước của m
=>\(m⋮n\)
NL
1
8 tháng 9 2016
Ta có:
S1 + S2 + S3 + ... + S2012 + S2013
= S( 1 + 2 + 3 + ... + 2012 + 2013 )
Đặt A = 1 + 2 + 3 + ... + 2012 + 2013
A = 2013 + 2012 + 2011 + ... + 1
2A = ( 1 + 2013 ) + ( 2 + 2012 ) + ( 3 + 2011 ) + ... ( 2013 + 1 ) ( 2013 cặp số )
2A = 2014 + 2014 + 2014 + ... + 2014 ( 2013 số 2014 )
2A = 2014 . 2013
2A = 4054182
A = 2027091
\(\Rightarrow\) Tổng S1 + S2 + S3 + ... + S2012 + S2013 là S2027091
1 tháng 8 2019
Câu c bạn tham khảo tại đây:
Câu hỏi của Edogawa Conan - Toán lớp 6 - Học toán với OnlineMath
21 tháng 3 2023
program TongSn;
var
N, S: integer;
begin
S := 0;
N := 1;
while S <= 1000 do
begin
S := S + N;
N := N + 1;
end;
writeln('So tu nhien can cong de tong Sn vuot qua 1000 la: ', N-1);
writeln('Tong S', N-1, ' la: ', S);
end.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d=n\left(n.\dfrac{d}{2}+u_1-\dfrac{d}{2}\right)=n\left(n+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{d}{2}=1\\u_1-\dfrac{d}{2}=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=5\\d=1\end{matrix}\right.\)
\(u_n=5+1.\left(n-1\right)=n+4\)