Mọi người làm nhanh giúp mik vs ah 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$
S
1
A
15 tháng 3 2022
0,5 × 3,16 × 4 × 2 × 0,25
= ( 0,5 × 2 ) × ( 0,25 × 4 ) × 3,16
= 1 × 1 × 3,16
= 1 × 3,16
= 3,16
6 tháng 7 2021
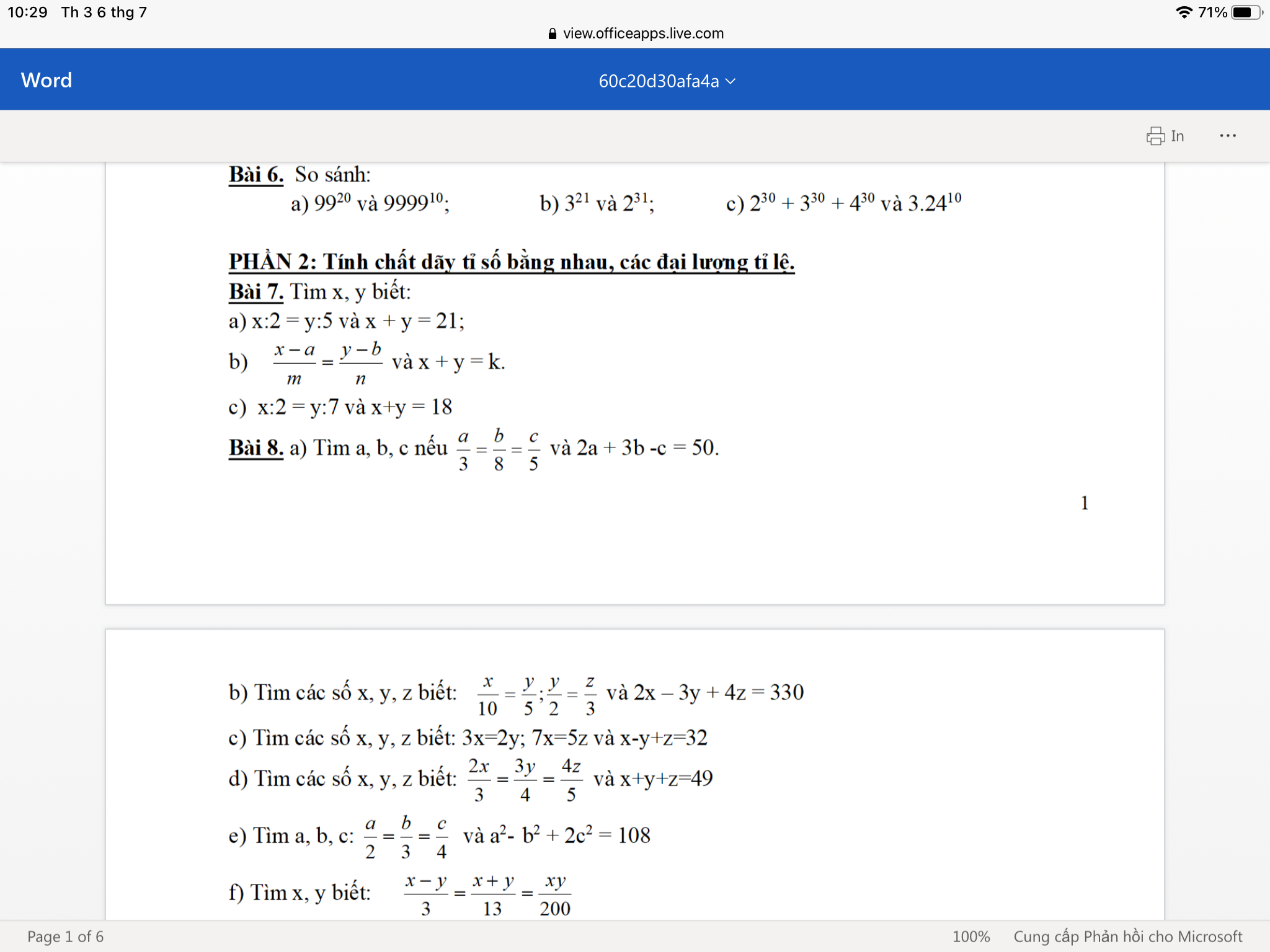
Bài 7:
a) Ta có: x:2=y:5
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=3\\\dfrac{y}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=15\end{matrix}\right.\)
c) Ta có: x:2=y:7
nên \(\dfrac{x}{2}=\dfrac{y}{7}\)
mà x+y=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{x+y}{2+7}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=2\\\dfrac{y}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=14\end{matrix}\right.\)
Bài 8:
a) Ta có: \(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\)
nên \(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}\)
mà 2a+3b-c=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}=\dfrac{2a+3b-c}{6+24-5}=\dfrac{50}{25}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{8}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=16\\c=10\end{matrix}\right.\)
6 tháng 7 2021
Bài 8:
b) Ta có: \(\dfrac{x}{10}=\dfrac{y}{5}\)
nên \(\dfrac{x}{20}=\dfrac{y}{10}\)(1)
Ta có: \(\dfrac{y}{2}=\dfrac{z}{3}\)
nên \(\dfrac{y}{10}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
\(\Leftrightarrow\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}\)
mà 2x-3y+4z=330
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}=\dfrac{2x-3y+4z}{40-30+60}=\dfrac{330}{70}=\dfrac{33}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=\dfrac{33}{7}\\\dfrac{y}{10}=\dfrac{33}{7}\\\dfrac{z}{15}=\dfrac{33}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{660}{7}\\y=\dfrac{330}{7}\\z=\dfrac{495}{7}\end{matrix}\right.\)
c) Ta có: 3x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
hay \(\dfrac{x}{10}=\dfrac{y}{15}\)(1)
Ta có: 7x=5z
nên \(\dfrac{x}{5}=\dfrac{z}{7}\)
hay \(\dfrac{x}{10}=\dfrac{z}{14}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x-y+z}{10-15+14}=\dfrac{32}{9}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{10}=\dfrac{32}{9}\\\dfrac{y}{15}=\dfrac{32}{9}\\\dfrac{z}{14}=\dfrac{32}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{320}{9}\\y=\dfrac{480}{9}=\dfrac{160}{3}\\z=\dfrac{448}{9}\end{matrix}\right.\)
XO
27 tháng 7 2020
Gọi số tự nhiên cần tìm là a
Ta có : \(\hept{\begin{cases}a⋮5\\a⋮7\\a⋮9\end{cases}}\Rightarrow a\in BC\left(5;7;9\right)\)
mà a nhỏ nhất có thể
=> \(a=BCNN\left(5;7;9\right)\)
Vì ƯCLN(5;7;9) = 1
=> BCNN(5;7;9) = 5.7.9 = 315
=> a = 315
Vậy số cần tìm là 315
27 tháng 7 2020
Gọi số tự nhiên cần tìm là a
Theo đề bài : a chia hết cho 5 , a chia hết cho 7 , a chia hết cho 9 và a là số tự nhiên nhỏ nhất
=> a = BCNN(5, 7 , 9 )
BCNN(5, 7 , 9) = 5 . 7 . 32 = 315
=> a = 315
Vậy số cần tìm là 315
MT
2
KV
2 tháng 5 2023
Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5
TP
1
24 tháng 8 2023
6:
Số tiền phải trả góp là:
350000*24=8400000(đồng)
Số tiền mua chiếc TV là:
8400000:60%=14000000(đồng)
28 tháng 5 2022
bạn ơi trong olm không có cái đó ạ phân số trong olm chỉ được biểu thị bằng dấu gạch chéo thôi nếu muốn dùng phân số theo ý bạn thì phải dùng latex nhưng trong olm không có latex cái này thì tùy thuộc vào olm chế ra thôi chứ mình cũng không phải Admin nên ko biết rõ lắm
c, (4 + 1\(\dfrac{3}{5}\)) . 2\(\dfrac{1}{7}\) - 4\(\dfrac{2}{3}\): \(\dfrac{5}{9}\)
= (4 + \(\dfrac{8}{5}\)) . \(\dfrac{15}{7}\) - \(\dfrac{14}{3}\): \(\dfrac{5}{9}\)
= \(\dfrac{28}{5}\). \(\dfrac{15}{7}\) - \(\dfrac{42}{5}\)
= 12 - \(\dfrac{42}{5}\)
= \(\dfrac{18}{5}\)