Một chất điểm dao động điều hòa trên trục Ox với tần số góc 10 (rad/s) và biên độ 10 (cm). Trong khoảng thời gian 0,2 (s), quãng đường lớn nhất và nhỏ nhất mà vật có thể đi được lần lượt là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
3 tháng 10 2018
Đáp án D
Chất điểm chuyển động chia đường tròn thành 12 cung, thời gian chuyển động trên mỗi cung tròn là t = T/12 = 0,1 s.
→ chu kì dao động của chất điểm là T = 12.t = 12.0,1 = 1,2 s
→ t = 0,8 s = 2T/3 = T/2 + T/6 → s = 2A + ∆s
Để tốc độ trung bình lớn nhất thì
= A/2 + A/2 = A
→ s = 2A + A = 3A = 30 cm
= 37,5 cm/s
VT
13 tháng 10 2017
Đáp án A
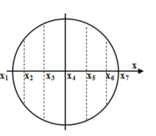
+ Gia tốc của vật cực đại tại vị trí biên âm → x 1 = - A .
Vật đi từ x 1 → x 7 hết nửa chu kì, vậy x 7 = + A → các vị trí liên tiếp các nhau ứng với góc quét 30 ° → Δx max .
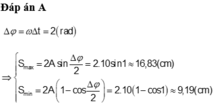
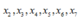
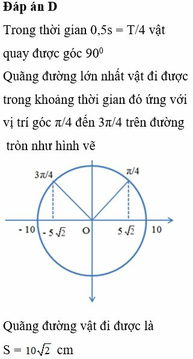
\(\Delta\varphi=\omega\Delta t=2\left(rad\right)\) \(\Rightarrow\) \(\left\{{}\begin{matrix}\text{S}_{max}=2Asin\dfrac{\Delta\varphi}{\text{2}}=2.10sin1\approx\text{16,83(cm)}\\\text{S}_{\text{min}}=\text{2A}\left(\text{1-cos}\dfrac{\Delta\varphi}{\text{2}}\right)=2.10\left(\text{1-cos1}\right)\approx\text{9,19(cm)}\end{matrix}\right.\)
Tham khảo:
\(\Delta\varphi=\omega\Delta t=2\left(rad/s\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}S_{max}=2Asin\dfrac{\Delta\varphi}{2}=2\cdot10sin1\approx16,8\left(cm\right)\\S_{min}=2A\left(1-cos\dfrac{\Delta\varphi}{2}\right)=2\cdot10\cdot\left(1-cos1\right)\approx9,19\left(cm\right)\end{matrix}\right.\)