một chất điểm dao động điều hòa theo pt x=4cos(\(\dfrac{2\pi t}{3}\)) (x tính bằng cm, t tính bằng s). kể từ t=0 chất điểm đi qua vị trí có li độ x=-2cm lần thứ 2011 tại thời điểm?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 12 2017
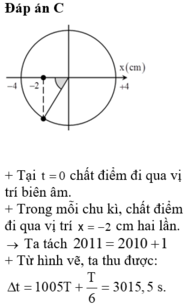
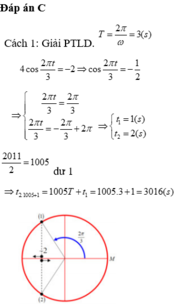
Đáp án C
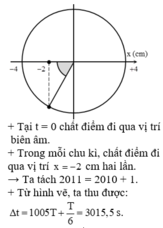
Tại t = 0 chất điểm đi qua vị trí biên âm.
Trong mỗi chu kì, chất điểm đi qua vị trí x = - 2 cm hai lần.
Ta tách 2011 = 2010 + 1
Từ hình vẽ, ta thu được:
VT
14 tháng 11 2019
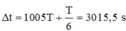
Đáp án B
Chu kì dao động của chất điểm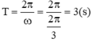 
Ta có hình vẽ
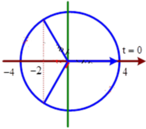
Một chu kì vật đi qua vị trí x = - 2 cm hai lần. Từ hình vẽ ta thấy, để vật đi qua vị trí x = -2 cm lần thứ 2019 cần thời gian 1009T + T/3 = 3028s
VT
6 tháng 8 2019
Chọn D.
Cách 1: Giải PTLG. T = 2 π ω = 3
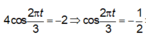
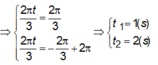
2017 2 = 1008 d ư 1
Cách 2: Dùng VTLG
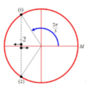
Quay một vòng qua li độ x = -2 cm là hai lần. Để có lần thứ
2017 = 2.1008 + 1 thì phải quay 1008 vòng và quay thêm một góc 2 π / 3 tức tổng góc quay: ∆ φ = 1008 . 2 π + 2 π / 3
thời gian:
VT
7 tháng 9 2018
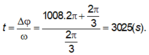
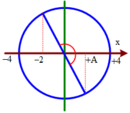
Biểu diễn dao động tương ứng trên đường tròn
Tại t = 0, chất điểm đi qua vị trí x=A/2=2cm theo chiều dương
Trong mỗi chu kì chất điểm đi qua vị trí x = -2 hai lần
Ta tách: 2019 = 2018 + 1 → 2018 lần ứng với 1009T
→ Tổng thời gian t=1009T+T/2=2019s
Chọn đáp án A
Ta có: \(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\dfrac{2\pi}{3}}=3\left(s\right)\)
Thời gian vật đi từ vị trí có li độ x = 4 cm đến vị trí có li độ x = -2 lần đầu tiên là:
\(t_1=\dfrac{T}{4}+\dfrac{T}{12}=\dfrac{3}{4}+\dfrac{3}{12}=1\left(s\right)\)
Thời gian vật đi qua vị trí có li độ x = -2 lần thứ 2 đến vị trí có li độ x = -2 lần thứ 2011 là:
\(t_2=1005\cdot T=1005\cdot3=3015\left(s\right)\)
Tổng thời gian cần là: \(t=t_1+t_2=1+3015=3016\left(s\right)\)