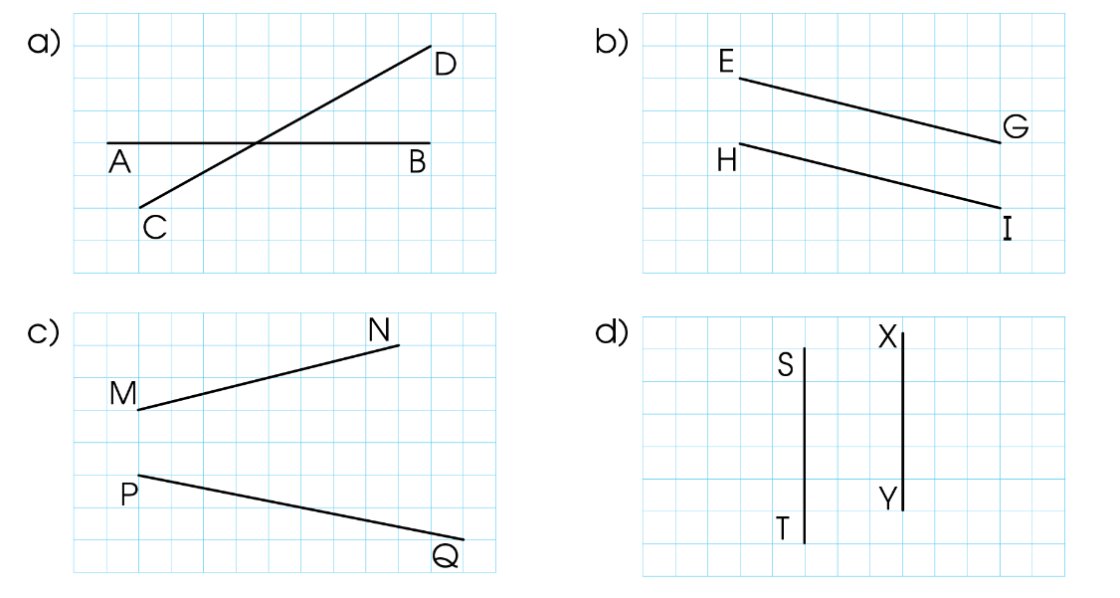
Nêu các cặp đường thẳng song song với nhau, các cặp đường thẳng không song song với nhau trong mỗi hình dưới đây:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
Các hình có các cặp đường thẳng song song với nhau: c, e
Các hình có các cặp đường thẳng vuông góc với nhau: b, d, g
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).
CM
21 tháng 8 2019
Giả sử a cắt yy’ tại E và b cắt xx’ tại F.
- Một số cặp góc bằng nhau:
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
Hệ số góc của đường thẳng \({d_1}:y = 3x\) là \(a = 3\);
Hệ số góc của đường thẳng \({d_2}:y = - 7x + 9\) là \(a = - 7\);
Hệ số góc của đường thẳng \({d_3}:y = 3x - 0,8\) là \(a = 3\);
Hệ số góc của đường thẳng \({d_4}:y = - 7x - 1\) là \(a = - 7\);
Hệ số góc của đường thẳng \({d_5}:y = \sqrt 2 x + 10\) là \(a = \sqrt 2 \);
Hệ số góc của đường thẳng \({d_6}:y = \sqrt 2 x + \sqrt {10} \) là \(a = \sqrt 2 \);
- Các cặp đường thẳng song song là:
\({d_1}:y = 3x\) và \({d_3}:y = 3x - 0,8\) vì đều có hệ số góc \(a = 3\) và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
\({d_2}:y = - 7x + 9\) và \({d_4}:y = - 7x - 1\) vì đều có hệ số góc \(a = - 7\)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
\({d_5}:y = \sqrt 2 x + 10\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì đều có hệ số góc \(a = \sqrt 2 \)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
- Ba cặp đường thẳng cắt nhau là:
\({d_1}:y = 3x\) và \({d_4}:y = - 7x - 1\) vì có hệ số góc khác nhau \(\left( {3 \ne - 7} \right)\).
\({d_2}:y = - 7x + 9\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì có hệ số góc khác nhau \(\left( { - 7 \ne \sqrt 2 } \right)\).
\({d_3}:y = 3x - 0,8\) và \({d_5}:y = \sqrt 2 x + 10\) vì có hệ số góc khác nhau \(\left( {3 \ne \sqrt 2 } \right)\).
CM
1 tháng 8 2019
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:
Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.
CM
23 tháng 7 2018
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:
Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.
CM
2 tháng 12 2017
a)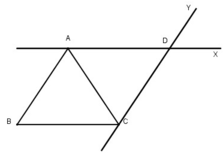
b) Các cặp cạnh song song với nhau có trong hình tứ giác ADCB là: cặp cạnh AD và BC, AB và DC.
`a, AB` không song song `CD`
`b, EG` song song `HI`
`c, MN` không song song `PQ`
`d, ST` song song `XY`